题目内容
17.化简(1)(9a-2b)-[8a-(5b-2a)]+2c
(2)(-x2+3xy-$\frac{1}{2}$y2)-(-$\frac{1}{2}$x2+4xy)
分析 根据整式加减的法则即可求出答案.
解答 解:(1)原式=9a-2b-(10a-5b)+2c=9a-2b-10a+5b+2c=-a+3b+2c,
(2)原式=-x2+3xy-$\frac{1}{2}$y2+$\frac{1}{2}$x2-4xy=-$\frac{1}{2}$x2-xy-$\frac{1}{2}$y2,
点评 本题考查整式加减运算,属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.以下列各组数据为三角形三边,不能构成三角形的是( )
| A. | 4,8,7 | B. | 3,4,7 | C. | 2,3,4 | D. | 13,12,5 |
12.下列说法中,正确的是( )
| A. | 方程5x2=x有两个不相等的实数根 | |
| B. | 方程x2-8=0有两个相等的实数根 | |
| C. | 方程2x2-3x+2=0有两个整数根 | |
| D. | 当k>$\frac{2}{3}$时,方程(k-1)x2+2x-3=0有两个不相等的实数根 |
2.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
下列结论:
(1)ac<0;
(2)抛物线顶点坐标为(1,5);
(3)3是方程ax2+(b-1)x+c=0的一个根;
(4)当-1<x<3时,ax2+(b-1)x+c>0.
其中正确的个数为( )
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
(1)ac<0;
(2)抛物线顶点坐标为(1,5);
(3)3是方程ax2+(b-1)x+c=0的一个根;
(4)当-1<x<3时,ax2+(b-1)x+c>0.
其中正确的个数为( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
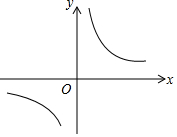 已知:Rt△ABC中,∠C=90°,∠B=60°,且BC=1,若把△ABC放入如图的直角坐标系中,使斜边AB在x轴,点C在双曲线y=$\frac{\sqrt{3}}{x}$上.
已知:Rt△ABC中,∠C=90°,∠B=60°,且BC=1,若把△ABC放入如图的直角坐标系中,使斜边AB在x轴,点C在双曲线y=$\frac{\sqrt{3}}{x}$上.