题目内容
平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4)B(2,4)C(3,-1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△DEF与△ABC关于x轴对称,写出D、E、F的坐标.
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△DEF与△ABC关于x轴对称,写出D、E、F的坐标.
考点:坐标与图形性质
专题:
分析:(1)根据三点的坐标,在直角坐标系中分别标出位置即可.
(2)以AB为底,则点C到AB的距离即是底边AB的高,结合坐标系可得出高为点C的纵坐标的绝对值加上点B的纵坐标的绝对值,从而根据三角形的面积公式计算即可.
(3)关于x轴对称的点的坐标,横坐标不变,纵坐标互为相反数,从而可得出D、E、F的坐标.
(2)以AB为底,则点C到AB的距离即是底边AB的高,结合坐标系可得出高为点C的纵坐标的绝对值加上点B的纵坐标的绝对值,从而根据三角形的面积公式计算即可.
(3)关于x轴对称的点的坐标,横坐标不变,纵坐标互为相反数,从而可得出D、E、F的坐标.
解答:解:(1)如图所示:

(2)由图形可得:AB=2,AB边上的高=|-1|+|4|=5,
∴△ABC的面积=
×2×5=5.
(3)∵A(0,4),B(2,4),C(3,-1),△DEF与△ABC关于x轴对称,
∴D(0,-4)、E(2,-4)、F(3,1).

(2)由图形可得:AB=2,AB边上的高=|-1|+|4|=5,
∴△ABC的面积=
| 1 |
| 2 |
(3)∵A(0,4),B(2,4),C(3,-1),△DEF与△ABC关于x轴对称,
∴D(0,-4)、E(2,-4)、F(3,1).
点评:本题考查了坐标与图形性质,轴对称作图,三角形的面积,难度一般,解答本题的关键是正确的找出三点的位置,另外要掌握关于x轴对称的点的坐标的特点.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
| 2 |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
 如图,△ABC中,BD平分∠ABC,AD⊥BD,D为垂足,E为AC的中点.
如图,△ABC中,BD平分∠ABC,AD⊥BD,D为垂足,E为AC的中点.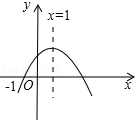 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0,②4a-2b+c<0,③ac>0,④当-1<x<3时,y>0,⑤当x≥1时,y随x的增大而增大,正确结论的序号是
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0,②4a-2b+c<0,③ac>0,④当-1<x<3时,y>0,⑤当x≥1时,y随x的增大而增大,正确结论的序号是 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上. 如图,将长方形ABCD沿直线AE折叠,顶点D恰好落在BC边上点F处.已知CE=3cm,AB=8cm. 求:
如图,将长方形ABCD沿直线AE折叠,顶点D恰好落在BC边上点F处.已知CE=3cm,AB=8cm. 求: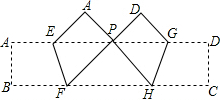 如图所示,折叠矩形纸条ABCD,使B,C两点落在AD边的P点处,折痕为EF,GH,若∠FPH的度数恰好为90°,PF=8,PH=6,则矩形ABCD的边BC的长为( )
如图所示,折叠矩形纸条ABCD,使B,C两点落在AD边的P点处,折痕为EF,GH,若∠FPH的度数恰好为90°,PF=8,PH=6,则矩形ABCD的边BC的长为( ) 市政府大力扶持节能环保产业,某企业研发出一种节能环保产品,获得市政府提供的120万元无息贷款,用于该产品的生产与销售,并约定用该产口的利润逐步偿还无息贷款,已知该产口的生产成本为每件60元,员工每人每月的工资为3000元,公司每月需支付其他费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
市政府大力扶持节能环保产业,某企业研发出一种节能环保产品,获得市政府提供的120万元无息贷款,用于该产品的生产与销售,并约定用该产口的利润逐步偿还无息贷款,已知该产口的生产成本为每件60元,员工每人每月的工资为3000元,公司每月需支付其他费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,交AC于点E,且DE=5cm,求BC的长.
如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,交AC于点E,且DE=5cm,求BC的长.