题目内容
 如图,将长方形ABCD沿直线AE折叠,顶点D恰好落在BC边上点F处.已知CE=3cm,AB=8cm. 求:
如图,将长方形ABCD沿直线AE折叠,顶点D恰好落在BC边上点F处.已知CE=3cm,AB=8cm. 求:(1)AD的长;
(2)阴影部分的面积.
考点:翻折变换(折叠问题)
专题:
分析:(1)证明△ABF∽△FCE,列出比例式
=
,求出AF=10,得到AD=AF=10.
(2)运用S阴影=10×8-2×
×10×5=80-50=30,即可解决问题.
| AB |
| CF |
| AF |
| EF |
(2)运用S阴影=10×8-2×
| 1 |
| 2 |
解答: 解:(1)如图,∵CD=AB=8,CE=3,
解:(1)如图,∵CD=AB=8,CE=3,
∴EF=DE=8-3=5;
由勾股定理得:CF=4;
由题意得:AF=AD(设为λ),∠AFE=∠D=90°;
∵∠B=∠C=90°;
∴∠BAF+∠AFB=∠AFB+∠EFC,
∴∠BAF=∠EFC,而∠B=∠C,
∴△ABF∽△FCE,
∴
=
,解得:AF=10.
∴AD=AF=10.
(2)由题意得:S△AEF=S△ADE,
∴S阴影=S矩形ABCD-2S△ADE
=10×8-2×
×10×5
=80-50=30.
 解:(1)如图,∵CD=AB=8,CE=3,
解:(1)如图,∵CD=AB=8,CE=3,∴EF=DE=8-3=5;
由勾股定理得:CF=4;
由题意得:AF=AD(设为λ),∠AFE=∠D=90°;
∵∠B=∠C=90°;
∴∠BAF+∠AFB=∠AFB+∠EFC,
∴∠BAF=∠EFC,而∠B=∠C,
∴△ABF∽△FCE,
∴
| AB |
| CF |
| AF |
| EF |
∴AD=AF=10.
(2)由题意得:S△AEF=S△ADE,
∴S阴影=S矩形ABCD-2S△ADE
=10×8-2×
| 1 |
| 2 |
=80-50=30.
点评:该题主要考查了旋转变换的性质及其应用、勾股定理及其应用等问题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
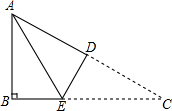 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )
如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 已知一个立体图形的三视图如图所示,现沿它的同一顶点的三条棱将其剪开展成平面图形,则所得到的平面展开图是下列图中的( )
已知一个立体图形的三视图如图所示,现沿它的同一顶点的三条棱将其剪开展成平面图形,则所得到的平面展开图是下列图中的( )



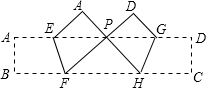 把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少?
把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少? 如图,AB∥CD,∠B:∠O:∠D=4:3:3,则∠B=
如图,AB∥CD,∠B:∠O:∠D=4:3:3,则∠B= 某工厂要赶制一批抗震救灾用的大型活动板房,如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为3.6m.
某工厂要赶制一批抗震救灾用的大型活动板房,如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为3.6m.