题目内容
18.先化简,再求值:($\frac{5}{a+2}$-a+2)÷$\frac{{{a^2}-6a+9}}{a+2}$,其中a=4.分析 先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
解答 解:原式=$\frac{5-{a}^{2}+4}{a+2}$•$\frac{a+2}{(a-3)^{2}}$
=$\frac{-(a+3)(a-3)}{a+2}$•$\frac{a+2}{{(a-3)}^{2}}$
=-a-3.
当a=4时,原式=-4-3=-7.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
3.一个多边形的边数增加1条,则它的内角和增加( )
| A. | 180° | B. | 90° | C. | 360° | D. | 540° |
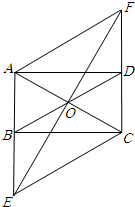 如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F.
如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F. 如图,△ABC中,AD是∠CAB的角平分线,DE∥AB,DF∥AC.问:DA平分∠EDF吗?为什么?
如图,△ABC中,AD是∠CAB的角平分线,DE∥AB,DF∥AC.问:DA平分∠EDF吗?为什么? 将等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠1=41°,∠2=51°,那么∠3的度数等于10°.
将等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠1=41°,∠2=51°,那么∠3的度数等于10°.