题目内容
9.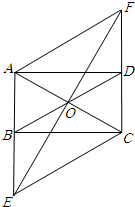 如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F.
如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F.(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么关系时,四边形AECF是菱形?证明你的结论;
(3)若四边形AECF是菱形,AB=6,BC=8,求EF的长.
分析 (1)根据四边形ABCD是矩形可证明△BOE≌△DOF,从而即可得出答案;
(2)先证明四边形AECF是平行四边形,然后根据菱形的判定性质即可证明;
(3)先证明△ABC∽△AOE,得出比例式求出OE,即可求出EF.
解答 (1)证明:∵四边形ABCD是矩形,
∴OB=OD,AB∥CD,
∴∠BEO=∠DFO,
在△BOE与△DOF中,
$\left\{\begin{array}{l}{∠BEO=∠DFO}\\{∠BOE=∠DOF}\\{OB=OD}\end{array}\right.$,
∴△BOE≌△DOF(AAS);
(2)解:当EF⊥AC时,四边形AECF是菱形;
证明:∵四边形ABCD是矩形,
∴OA=OC,
由(1)知OE=OF,则四边形AECF是平行四边形,
又∵EF⊥AC,
∴四边形AECF是菱形;
(3)解:∵四边形AECF是菱形,
∴AC⊥EF,OE=$\frac{1}{2}$EF,
∴∠AOE=90°,
∴∠OAE+∠AEO=90°,
∵∠ABC=90°,
∴∠OAE+∠ACB=90°,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴OA=$\frac{1}{2}$AC=5,∠AEO=∠ACB,
∴△ABC∽△AOE,
∴$\frac{BC}{OE}=\frac{AB}{OA}$,即$\frac{8}{OE}=\frac{6}{5}$,
∴OE=$\frac{20}{3}$,
∴EF=2OE=$\frac{40}{3}$.
点评 本题考查了菱形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质;证明三角形全等和三角形相似是解决问题的关键.

练习册系列答案
相关题目
19.某商店有两个进价不同的计算器都卖了80元,其中一个盈利60%,另一个亏本20%,在这次买卖中,这家商店( )
| A. | 赚了50元 | B. | 赚了10元 | C. | 赔了10元 | D. | 不赔不赚 |
 如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.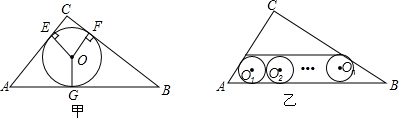
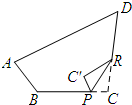 如图,将四边形纸片ABCD的右下角向内折出△PC′R,其中∠B=120°,∠D=40°,恰使C′P∥AB,RC′∥AD,则∠C=100°.
如图,将四边形纸片ABCD的右下角向内折出△PC′R,其中∠B=120°,∠D=40°,恰使C′P∥AB,RC′∥AD,则∠C=100°. 如图,把边长为6cm的正方形ABCD先向右平移2cm,再向上平移1cm,得到正方形EFGH,则阴影部分的面积为20平方厘米.
如图,把边长为6cm的正方形ABCD先向右平移2cm,再向上平移1cm,得到正方形EFGH,则阴影部分的面积为20平方厘米.