题目内容
14. 如图,⊙O的弦AB,CE相交于点E,且B恰好是$\widehat{CD}$的中点,连接AC,BD,BC.求证:BD2=AB•BE.
如图,⊙O的弦AB,CE相交于点E,且B恰好是$\widehat{CD}$的中点,连接AC,BD,BC.求证:BD2=AB•BE.
分析 根据圆周角定理得到∠A=∠BCD,BD=BC,根据相似三角形的性质得到BC2=AB•EB,等量代换即可得到结论.
解答 证明:∵B是$\widehat{CD}$的中点,
∴$\widehat{BC}$=$\widehat{BD}$,
∴∠A=∠BCD,BD=BC,
∵∠CBA=∠EBC,
∴△CEB∽△ACB,
∴$\frac{EB}{BC}=\frac{BC}{AB}$,
∴BC2=AB•EB,
∵BD=BC,
∴BD2=AB•BE.
点评 本题考查了相似三角形的判定和性质,圆周角定理,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
9.等腰三角形ABC中,AB=CB=5,AC=8,P为AC边上一动点,PQ⊥AC,PQ与△ABC的腰交于点Q,连结CQ,设AP为x,△CPQ面积为y,则y关于x的函数关系的图象大致是( )
| A. | 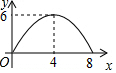 | B. | 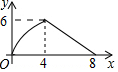 | C. | 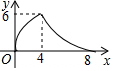 | D. | 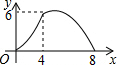 |
3.学校新开设了航模、彩绘两个社团,如果征征、舟舟两名同学每人随机选择参加其中一个社团,那么征征和舟舟选到同一社团的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
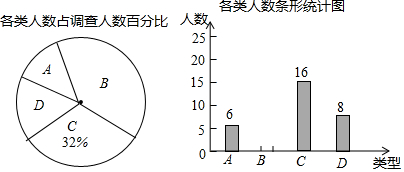
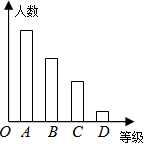 某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:
某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题: