题目内容
2.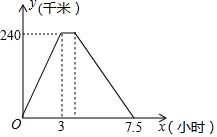 小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离y(千米)和所用的时间x(小时)之间的函数关系如图所示.
小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离y(千米)和所用的时间x(小时)之间的函数关系如图所示.(1)小李从乙地返回甲地用了多少小时?
(2)求小李出发6小时后距离甲地多远?
(3)在甲、乙两地之间有一丙地,小李从去时途经丙地,到返回时路过丙地,共用了2小时50分钟,求甲、丙两地相距多远?
分析 (1)根据题意和函数图象可以求得小李从乙地返回甲地用的时间;
(2)根据题意和函数图象中的数据可以求得小李从乙地返回甲地对应的函数解析式,从而可以求得小李出发6小时后距离甲地的距离;
(3)根据题意可以列出相应的方程,从而可以求得甲、丙两地的距离.
解答 解:(1)由题意可得,
小李从乙地返回甲地用的时间为:7.5-(3+0.5)=4(小时),
答:小李从乙地返回甲地用了4小时;
(2)设小李从乙地返回甲地对应的函数解析式为y=kx+b,
$\left\{\begin{array}{l}{3.5k+b=240}\\{7.5k+b=0}\end{array}\right.$,得$\left\{\begin{array}{l}{k=-60}\\{b=450}\end{array}\right.$,
即小李从乙地返回甲地对应的函数解析式为y=-60x+450,
将x=6代入y=-60x+450,得y=90,
答:小李出发6小时后距离甲地90千米;
(3)设从甲地到乙地的过程中到达丙地的时间为x小时,
从甲地到乙地的速度为:240÷3=80千米/时,
则80x=-60(x+2$\frac{50}{60}$)+450,
解得,x=2,
∴80x=160,
答:甲、丙两地相距160千米.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质和数形结合的思想解答.

练习册系列答案
相关题目
13.某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4290元,且销售完这批商品后获利多于1260元,请问共有几种购货方案?
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
(2)若商店计划投入资金少于4290元,且销售完这批商品后获利多于1260元,请问共有几种购货方案?
11.计算(-1)2017+(-$\frac{1}{2}$)-3-(2017)0的结果是( )
| A. | -10 | B. | -8 | C. | 8 | D. | -9 |
12.在平面直角坐标系中,点(-6,-1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 ≥-2的解集,正确的是( )
≥-2的解集,正确的是( ) B.
B.  C.
C.  D.
D. 
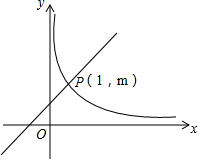 如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=$\frac{2}{x}$(x>0)相交于P(1,m).
如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=$\frac{2}{x}$(x>0)相交于P(1,m).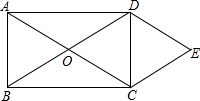 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.