题目内容
 如图,是一个由4条线段构成“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线段,并说明理由.
如图,是一个由4条线段构成“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线段,并说明理由.考点:平行线的判定
专题:
分析:由∠1=∠2可判定OA∥BC;由∠3+∠ACB=180°可判定OB∥AC.
解答:解:OA∥BC,OB∥AC.
理由:∵∠1=∠2=50°,
∴OA∥BC;
∵∠2=50°,
∴∠ACB=∠2=50°,
∴∠ACB+∠3=50°+130°=180°,
∴OB∥AC.
理由:∵∠1=∠2=50°,
∴OA∥BC;
∵∠2=50°,
∴∠ACB=∠2=50°,
∴∠ACB+∠3=50°+130°=180°,
∴OB∥AC.
点评:本题主要考查平行线的判定,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,下列条件能判定a∥b的是( )
如图,下列条件能判定a∥b的是( )| A、∠1=∠2 |
| B、∠1+∠2=180° |
| C、∠2+∠3=180° |
| D、∠3=∠4 |
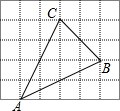 如图,网格中的每个小正方形的边长都是1,△ABC的每个顶点都在网格格点处,则sin∠CAB=
如图,网格中的每个小正方形的边长都是1,△ABC的每个顶点都在网格格点处,则sin∠CAB=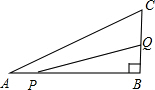 在△ABC中.∠B=90°,AB=6cm,BC=5cm,点P从点A开始,沿AB边向点B以1cm/s的速度移动,点Q从点B开始,沿BC边向点C以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发.经过多少秒后,△PBQ的面积等于8cm2?
在△ABC中.∠B=90°,AB=6cm,BC=5cm,点P从点A开始,沿AB边向点B以1cm/s的速度移动,点Q从点B开始,沿BC边向点C以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发.经过多少秒后,△PBQ的面积等于8cm2? 如图,在△ABC中,AB=12,AC=9,BC=10,点D是AB上的一个动点,若D以2个单位长度每秒的速度,从点B出发沿边BA向点A运动,过点D作DE∥BC,交AC于点E,记x秒时DE的长度为y,请写出y关于x的函数解析式,并求自变量x的取值范围.
如图,在△ABC中,AB=12,AC=9,BC=10,点D是AB上的一个动点,若D以2个单位长度每秒的速度,从点B出发沿边BA向点A运动,过点D作DE∥BC,交AC于点E,记x秒时DE的长度为y,请写出y关于x的函数解析式,并求自变量x的取值范围.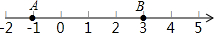 已知数轴上两点A、B对应的数分别为-1、3,数轴上一动点P对应的数为x
已知数轴上两点A、B对应的数分别为-1、3,数轴上一动点P对应的数为x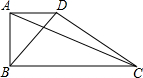 有一个零件如图所示,要求∠DAB,∠ABC都是直角,工人师傅量得AD=6,AB=8,BC=15,又量得BD=10,AC=17,这个零件符合要求吗,说说你的理由.
有一个零件如图所示,要求∠DAB,∠ABC都是直角,工人师傅量得AD=6,AB=8,BC=15,又量得BD=10,AC=17,这个零件符合要求吗,说说你的理由. 如图,∠ABC=∠BCD,∠1=∠2,求证:BE∥CF.
如图,∠ABC=∠BCD,∠1=∠2,求证:BE∥CF.