题目内容
等腰三角形底角是30°,腰长为2
,求它的周长.
| 3 |
考点:含30度角的直角三角形,等腰三角形的性质
专题:
分析:过A作AD⊥BC于D,根据含30度角的直角三角形性质求出AD,根据勾股定理求出BD、CD,即可求出答案.
解答: 解:过A作AD⊥BC于D,
解:过A作AD⊥BC于D,
则∠ADB=∠ADC=90°,
∵AB=AC=2
,∠B=30°,
∴AD=
AB=
,
由勾股定理得:BD=
=3,
同理CD=3,
∴BC=6,
∴△ABC的周长为BC+AB+AC=6+2
+2
=6+4
.
 解:过A作AD⊥BC于D,
解:过A作AD⊥BC于D,则∠ADB=∠ADC=90°,
∵AB=AC=2
| 3 |
∴AD=
| 1 |
| 2 |
| 3 |
由勾股定理得:BD=
(2
|
同理CD=3,
∴BC=6,
∴△ABC的周长为BC+AB+AC=6+2
| 3 |
| 3 |
| 3 |
点评:本题考查了勾股定理,等腰三角形的性质,含30度角的直角三角形性质的应用,解此题的关键是构造直角三角形,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
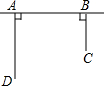 如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等.
如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等.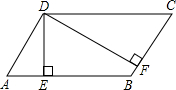 如图,已知平行四边形ABCD的周长为25cm,对边的距离分别为DE=2cm,DF=3cm,求:这个平行四边形的面积.
如图,已知平行四边形ABCD的周长为25cm,对边的距离分别为DE=2cm,DF=3cm,求:这个平行四边形的面积.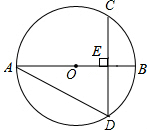 如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2.
如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2.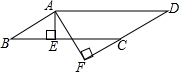 如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长.
如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长.
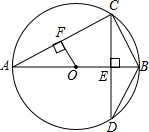 如图,AB为⊙O的直径,CD⊥AB,垂足为点E,交⊙O于点C和点D,OF⊥AC,垂足为点F.
如图,AB为⊙O的直径,CD⊥AB,垂足为点E,交⊙O于点C和点D,OF⊥AC,垂足为点F. 如图,是一个由4条线段构成“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线段,并说明理由.
如图,是一个由4条线段构成“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线段,并说明理由. 如图,由∠1=∠2,可以推出
如图,由∠1=∠2,可以推出