题目内容
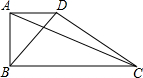 有一个零件如图所示,要求∠DAB,∠ABC都是直角,工人师傅量得AD=6,AB=8,BC=15,又量得BD=10,AC=17,这个零件符合要求吗,说说你的理由.
有一个零件如图所示,要求∠DAB,∠ABC都是直角,工人师傅量得AD=6,AB=8,BC=15,又量得BD=10,AC=17,这个零件符合要求吗,说说你的理由.考点:勾股定理的逆定理
专题:应用题
分析:根据勾股定理的逆定理,可判断△ABD、△ABC的形状,从而判断这个零件是否符合要求.
解答:解:这个零件符合要求,理由如下:
∵AD=6,AB=8,BC=15,BD=10,AC=17,
∴AB2+AD2=BD2,AB2+BC2=AC2,
∴△ABD,且∠DAB=90°,△ABC是直角三角形,∠ABC=90°.
故这个零件符合要求.
∵AD=6,AB=8,BC=15,BD=10,AC=17,
∴AB2+AD2=BD2,AB2+BC2=AC2,
∴△ABD,且∠DAB=90°,△ABC是直角三角形,∠ABC=90°.
故这个零件符合要求.
点评:本题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.关键是根据勾股定理的逆定理判断△ABD、△BDC的形状.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
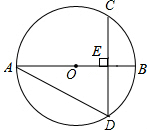 如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2.
如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2. 如图,是一个由4条线段构成“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线段,并说明理由.
如图,是一个由4条线段构成“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线段,并说明理由.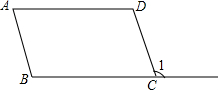 如图,分析图形,完成填空.
如图,分析图形,完成填空.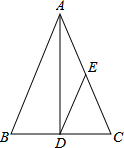 如图,在△ABC中,∠B=∠C,D,E分别是BC,AC的中点,AB=8,求DE的长.
如图,在△ABC中,∠B=∠C,D,E分别是BC,AC的中点,AB=8,求DE的长. 如图,由∠1=∠2,可以推出
如图,由∠1=∠2,可以推出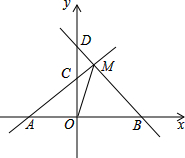 如图,A、B分别是x轴上位于原点左、右两侧的点,点M(2,P)在第一象限,直线MA交y轴于点C(0,3),直线MB交y轴于点D,S△AOM=9.
如图,A、B分别是x轴上位于原点左、右两侧的点,点M(2,P)在第一象限,直线MA交y轴于点C(0,3),直线MB交y轴于点D,S△AOM=9.