题目内容
 如图,在△ABC中,AB=12,AC=9,BC=10,点D是AB上的一个动点,若D以2个单位长度每秒的速度,从点B出发沿边BA向点A运动,过点D作DE∥BC,交AC于点E,记x秒时DE的长度为y,请写出y关于x的函数解析式,并求自变量x的取值范围.
如图,在△ABC中,AB=12,AC=9,BC=10,点D是AB上的一个动点,若D以2个单位长度每秒的速度,从点B出发沿边BA向点A运动,过点D作DE∥BC,交AC于点E,记x秒时DE的长度为y,请写出y关于x的函数解析式,并求自变量x的取值范围.考点:相似三角形的判定与性质,函数关系式,函数自变量的取值范围
专题:
分析:如图,证明△ADE∽△ABC,列出比例式
=
,即
=
,求出y即可解决问题.
| AD |
| AB |
| DE |
| BC |
| 12-2x |
| 12 |
| y |
| 10 |
解答: 解:如图,由题意得:BD=2x,AD=12-2x;
解:如图,由题意得:BD=2x,AD=12-2x;
∵DE∥BC,
∴△ADE∽△ABC,
∴
=
,即
=
,
∴y=-
x+10,0<x<12.
 解:如图,由题意得:BD=2x,AD=12-2x;
解:如图,由题意得:BD=2x,AD=12-2x;∵DE∥BC,
∴△ADE∽△ABC,
∴
| AD |
| AB |
| DE |
| BC |
| 12-2x |
| 12 |
| y |
| 10 |
∴y=-
| 5 |
| 3 |
点评:该题主要考查了相似三角形的判定及其性质、图形中的函数关系、自变量取值范围等知识点问题;解题的关键是数形结合,准确找出图形中隐含的数式信息,灵活运用相似三角形的判定及其性质来解题.

练习册系列答案
相关题目
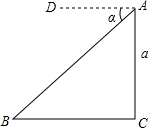 如图,飞机在空中A处探测得地面目标B处的俯角为α,此时飞机高度为AC=a,则BC的长度是( )
如图,飞机在空中A处探测得地面目标B处的俯角为α,此时飞机高度为AC=a,则BC的长度是( )| A、a•tanα | ||
B、
| ||
C、
| ||
D、
|
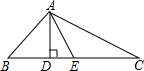 如图,△ABC中,AB=2,BC=5,AC=4.AD、AE分别为CB边上的高和中线,求DE的长.
如图,△ABC中,AB=2,BC=5,AC=4.AD、AE分别为CB边上的高和中线,求DE的长.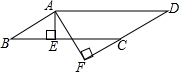 如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长.
如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长.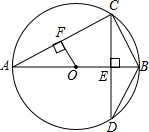 如图,AB为⊙O的直径,CD⊥AB,垂足为点E,交⊙O于点C和点D,OF⊥AC,垂足为点F.
如图,AB为⊙O的直径,CD⊥AB,垂足为点E,交⊙O于点C和点D,OF⊥AC,垂足为点F. 如图,是一个由4条线段构成“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线段,并说明理由.
如图,是一个由4条线段构成“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线段,并说明理由.