题目内容
(1)2x2-5x-1=0(公式法)
(2)x2-8x-10=0(配方法)
(3)2x2-2
x-5=0
(4)3y(y-1)=2(y-1)
(2)x2-8x-10=0(配方法)
(3)2x2-2
| 2 |
(4)3y(y-1)=2(y-1)
考点:解一元二次方程-因式分解法,解一元二次方程-配方法,解一元二次方程-公式法
专题:
分析:(1)求出b2-4ac的值,再代入公式求出即可;
(2)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(3)求出b2-4ac的值,再代入公式求出即可;
(4)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.
(2)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(3)求出b2-4ac的值,再代入公式求出即可;
(4)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.
解答:解:(1)2x2-5x-1=0,
b2-4ac=(-5)2-4×2×(-1)=33,
x=
,
x1=
,x2=
;
(2)x2-8x-10=0,
x2-8x=10,
x2-8x+42=10+42,
(x-4)2=26,
x-4=±
,
x1=4+
,x2=4-
;
(3)2x2-2
x-5=0,
b2-4ac=(-2
)2-4×2×(-5)=48,
x=
x1=
,x2=
;
(4)3y(y-1)=2(y-1),
3y(y-1)-2(y-1)=0,
(y-1)(3y-2)=0,
y-1=0,3y-2=0,
y1=1,y2=
.
b2-4ac=(-5)2-4×2×(-1)=33,
x=
5±
| ||
| 2×2 |
x1=
5+
| ||
| 4 |
5-
| ||
| 4 |
(2)x2-8x-10=0,
x2-8x=10,
x2-8x+42=10+42,
(x-4)2=26,
x-4=±
| 26 |
x1=4+
| 26 |
| 26 |
(3)2x2-2
| 2 |
b2-4ac=(-2
| 2 |
x=
2
| ||||
| 2×2 |
x1=
| ||||
| 2 |
| ||||
| 2 |
(4)3y(y-1)=2(y-1),
3y(y-1)-2(y-1)=0,
(y-1)(3y-2)=0,
y-1=0,3y-2=0,
y1=1,y2=
| 2 |
| 3 |
点评:本题考查了解一元二次方程的应用,主要考查学生的计算能力.

练习册系列答案
相关题目
在同圆中,若AB和CD都是劣弧,且AB=2CD,那么弦AB和CD的大小关系是( )
| A、AB=2CD |
| B、AB>2CD |
| C、AB<2CD |
| D、无法比较它们的大小 |
方程2x2+x-4=0的解的情况是( )
| A、有两个不相等的实数根 |
| B、没有实数根 |
| C、有两个相等的实数根 |
| D、有一个实数根 |
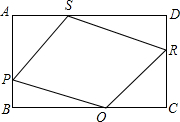 如图,在矩形ABCD中,AB=4,BC=8,菱形PQRS的四个顶点P、Q、R、S分别在矩形的边AB、BC、CD、DA上.
如图,在矩形ABCD中,AB=4,BC=8,菱形PQRS的四个顶点P、Q、R、S分别在矩形的边AB、BC、CD、DA上.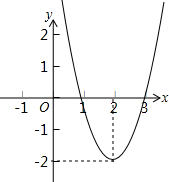 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题: