题目内容
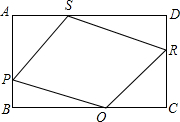 如图,在矩形ABCD中,AB=4,BC=8,菱形PQRS的四个顶点P、Q、R、S分别在矩形的边AB、BC、CD、DA上.
如图,在矩形ABCD中,AB=4,BC=8,菱形PQRS的四个顶点P、Q、R、S分别在矩形的边AB、BC、CD、DA上.(1)求证:△ASP≌CQR;
(2)设AS=x,AP=y,求y与x之间的函数解析式,并求出这个函数的定义域;
(3)当x取定义域中的最小值时,菱形PQRS的面积是多少?
考点:矩形的性质,全等三角形的判定与性质,菱形的性质
专题:
分析:(1)连接SQ,PR,相交于点O,连接BD,利用菱形的性质、矩形的性质即可证明:△ASP≌CQR;
(2)因为AS=x,所以可得SD=BQ=8-x,由勾股定理可得x2+y2=(8-x)2+(4-y)2,进而得到y和x的关系式;
(3)当x取定义域中的最小值时即x=2时,可求出PA,SO的长,进而可求出菱形的面积.
(2)因为AS=x,所以可得SD=BQ=8-x,由勾股定理可得x2+y2=(8-x)2+(4-y)2,进而得到y和x的关系式;
(3)当x取定义域中的最小值时即x=2时,可求出PA,SO的长,进而可求出菱形的面积.
解答:(1)证明:连接SQ,PR,相交于点O,连接BD.
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,AB=DC=5,AD=BC=10.
∵四边形PQRS是菱形,
∴SO=QO,PO=RO
∴点O是菱形的中心,也是矩形的中心.
∴BD过点O,
∴△SOD≌△QOB,△POB≌△ROD,
∴SD=BQ,PB=DR,AS=QC,AP=RC,
∴△ASP≌CQR;
(2)∵AS=x,SD=BQ=8-x,
∵AP=y,BP=4-y,
∴DR=x,AP=RC=5-x,
∴x2+y2=(8-x)2+(4-y)2,
∴y=10-2x,(3≤x≤5);
(3)∵x=2时,PR=4
,SO=
SQ=2
,
∴菱形PQRS的面积是20.

∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,AB=DC=5,AD=BC=10.
∵四边形PQRS是菱形,
∴SO=QO,PO=RO
∴点O是菱形的中心,也是矩形的中心.
∴BD过点O,
∴△SOD≌△QOB,△POB≌△ROD,
∴SD=BQ,PB=DR,AS=QC,AP=RC,
∴△ASP≌CQR;
(2)∵AS=x,SD=BQ=8-x,
∵AP=y,BP=4-y,
∴DR=x,AP=RC=5-x,
∴x2+y2=(8-x)2+(4-y)2,
∴y=10-2x,(3≤x≤5);
(3)∵x=2时,PR=4
| 5 |
| 5 |
| 5 |
∴菱形PQRS的面积是20.
点评:本题考查了矩形的性质,菱形的性质,全等三角形的判断和性质以及勾股定理的运用及二次函数的运用,题目的综合性较强,难度较大.

练习册系列答案
相关题目
已知x1、x2是方程x2-2x-1=0的两个根,则
+
的值为( )
| 1 |
| x1 |
| 1 |
| x2 |
A、-
| ||
| B、2 | ||
C、
| ||
| D、-2 |
 如图,∠C=90°,⊙C与AB相交于点D,AC=5,CB=12,则AD=
如图,∠C=90°,⊙C与AB相交于点D,AC=5,CB=12,则AD=