题目内容

设钝角△ABC三边分别是a、b、c，且∠C是钝角，求证：a2+b2＜c2．
考点：勾股定理
专题：证明题
分析：利用余弦定理，结合△ABC是钝角三角形，且∠C是钝角，即可证明a2+b2＜c2．
解答：证明：∵△ABC是钝角三角形，且∠C是钝角，
∴cosC＜0，
∵cosC=
a2+b2-c2
2ab
，
∴a2+b2＜c2．
点评：考查了勾股定理和余弦定理的运用，本题可以得到结论：钝角三角形中钝角所对的边的平方＞其余两条边的平方和．
练习册系列答案
相关题目
在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．
（1）当直线MN绕点C旋转到图1的位置时，DE，AD，BE的数量关系是
 
，并请给出证明过程．
（2）当直线MN绕点C旋转到图2的位置时，DE，AD，BE的数量关系是
 
（直接写出结果）．
解下列方程：
（1）
4
3
-8x=3-
11
2
x  
（2）0.5x-0.7=6.5-1.3x  
（3）
1
6
（3x-6）=
2
5
x-3   
（4）
1-2x
3
=
3x+1
7
-3．
计算：
（1）0.12530×（-8）30；
（2）24×44×（-0.125）4．
如图，直角坐标系内的梯形AOBC，AC∥OB，AC、OB的长分别是关于x的方程x2-6mx+m2+4=0的两根，并且S△AOC：S△BOC=1：5．
（1）求AC、OB的长；
（2）当BC⊥OC时，求OC的长及OC所在的直线解析式．
操作与探究：
数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．若将数轴画在纸面上，折叠纸面：
①若1表示的点和-1表示的点重合，则2表示的点与
 
表示的点重合；
②若3表示的点和-1表示的点重合，则5表示的点和
 
表示的点重合；数a表示的点与
 
表示的点重合（用a的代数式表示）；这时如果A、B两点之间的距离为6（A在B的左侧），且A、B两点经折叠后重合，则点A表示的数是
 
．
在△ABC中，AB=AC=13，BC=10，则△ABC的面积为（　　）
A、30B、60C、65D、120
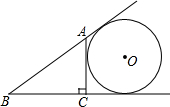如图，AC⊥BC于点C，⊙O与直线AB、BC、CA都相切，若⊙O的半径等于1，BC=2，△ABC的周长是
 
．
由8时15分到8时40分，时钟的分针旋转的角度为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网