题目内容
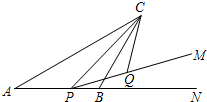 如图,△ABC中,AC=10,∠BAC=30°,点P是射线AB上的一个动点,cos∠CPM=
如图,△ABC中,AC=10,∠BAC=30°,点P是射线AB上的一个动点,cos∠CPM=| 4 |
| 5 |
考点:相似三角形的判定与性质
专题:动点型
分析:在△PCQ中,由cos∠CPM=
,可知当CP确定时则当CQ⊥PM时,CQ最小,而CP最小时则CQ也最小,故当CP⊥AN时,CP最小,由直角三角形的性质和三角函数的定义可求得CP的最小值为5,可求得CQ最小值为3.
| 4 |
| 5 |
解答: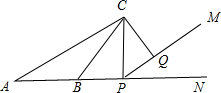 解:由题意可知当CP最小时,可知在△CPQ中当CQ⊥PM时,CQ有最小值,
解:由题意可知当CP最小时,可知在△CPQ中当CQ⊥PM时,CQ有最小值,
当CP⊥AN,CQ⊥PM时,如图,
在Rt△APC中,AC=10,∠BAC=30°,∴PC=5,
在Rt△CPQ中,cos∠CPM=
,∴PQ=4,
则可求得CQ=3,
故答案为:3.
 解:由题意可知当CP最小时,可知在△CPQ中当CQ⊥PM时,CQ有最小值,
解:由题意可知当CP最小时,可知在△CPQ中当CQ⊥PM时,CQ有最小值,当CP⊥AN,CQ⊥PM时,如图,
在Rt△APC中,AC=10,∠BAC=30°,∴PC=5,
在Rt△CPQ中,cos∠CPM=
| 4 |
| 5 |
则可求得CQ=3,
故答案为:3.
点评:本题主要考查直角三角形的性质及三角函数的定义,找到当CQ取得最小值时的点P和点Q的位置是解题的关键.

练习册系列答案
相关题目
在△ABC中,AB=AC=13,BC=10,则△ABC的面积为( )
| A、30 | B、60 | C、65 | D、120 |
正多边形的一个内角等于144°,则该多边形是正( )边形.
| A、8 | B、9 | C、10 | D、11 |
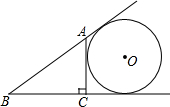 如图,AC⊥BC于点C,⊙O与直线AB、BC、CA都相切,若⊙O的半径等于1,BC=2,△ABC的周长是
如图,AC⊥BC于点C,⊙O与直线AB、BC、CA都相切,若⊙O的半径等于1,BC=2,△ABC的周长是