题目内容
15.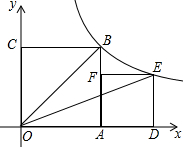 如图,两个正方形OABC、ADEF拼放于直角坐标系中,反比例函数y=$\frac{k}{x}(k≠0,x>0)$的图象经过B点和E点,已知△OEB的面积为2,则正方形ADEF的面积为( )
如图,两个正方形OABC、ADEF拼放于直角坐标系中,反比例函数y=$\frac{k}{x}(k≠0,x>0)$的图象经过B点和E点,已知△OEB的面积为2,则正方形ADEF的面积为( )| A. | 1 | B. | 6-2$\sqrt{5}$ | C. | $\sqrt{5}-1$ | D. | 3$\sqrt{5}$-5 |
分析 首先证明BD∥AE得S△OBE=S△AOB=2,得出B(2,2),反比例函数y=$\frac{4}{x}$,设正方形EFAD的边长为b,列出方程即可解决.
解答  解:∵四边形OABC、ADEF都是正方形,
解:∵四边形OABC、ADEF都是正方形,
∴∠EAD=∠BOA=45°,
∴OB∥AE,
∴S△OBE=S△AOB=2,
∴S正方形OABC=4,
∴OA=AB=2,
∴B(2,2).k=4,
反比例函数为y=$\frac{4}{x}$,
设正方形EFAD的边长为b,
∴E(2+b,b),
∴b(2+b)=4,
∴b2+2b-4=0,
∴b=$\sqrt{5}-1$(或-$\sqrt{5}$-1舍弃)
∴正方形EFAD的面积=b2=6-2$\sqrt{5}$.
故选B.
点评 本题考查反比例函数的有关性质、正方形的性质等知识,解题的关键是发现OB∥AE推出S△OBE=S△AOB,学会用方程的思想解决问题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.若m>n,则下列不等式成立的是( )
| A. | -3m>-2n | B. | am>an | C. | a2m>a2n | D. | m-3>n-3 |
6.“2x-1=x+●”是一个被墨水污染过的方程,答案显示次方程的解是x=3,被墨水遮盖的是一个常数,则这个常数是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
10.函数y=$\frac{1}{3}{x}^{2}$+1与y=$\frac{1}{3}{x}^{2}$的图象的不同之处是( )
| A. | 对称轴 | B. | 开口方向 | C. | 顶点 | D. | 形状 |
7.下列三个说法中:
(1)两点确定一条直线;
(2)同角(等角)的补角相等;
(3)两点之间,直线最短.
其中正确的个数是( )
(1)两点确定一条直线;
(2)同角(等角)的补角相等;
(3)两点之间,直线最短.
其中正确的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
4.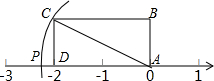 如图,长方形ABCD的边AB=1,BC=2,AP=AC,则点P所表示的数是( )
如图,长方形ABCD的边AB=1,BC=2,AP=AC,则点P所表示的数是( )
 如图,长方形ABCD的边AB=1,BC=2,AP=AC,则点P所表示的数是( )
如图,长方形ABCD的边AB=1,BC=2,AP=AC,则点P所表示的数是( )| A. | 5 | B. | -2.5 | C. | $\sqrt{5}$ | D. | $-\sqrt{5}$ |

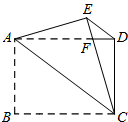 如图,将矩形ABCD沿对角线AC折叠,使点B与点E重合,EC与AD交于点F,连结ED.
如图,将矩形ABCD沿对角线AC折叠,使点B与点E重合,EC与AD交于点F,连结ED.