题目内容
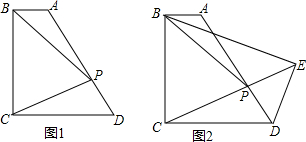
5. 如图,将矩形ABCD沿对角线AC折叠,使点B与点E重合,EC与AD交于点F,连结ED.
如图,将矩形ABCD沿对角线AC折叠,使点B与点E重合,EC与AD交于点F,连结ED.(1)求证:ED∥AC;
(2)若AB=3,BC=4,求四边形ACDE的面积.
分析 (1)欲证明ED∥AC,只要证明∠DAC=∠EDF即可.
(2)设AF的长为x,在RT△DFC中利用勾股定理求出x得AF:DF=25:7,利用$\frac{{{S_{△EDC}}}}{{{S_{△AEC}}}}=\frac{ED}{AC}=\frac{DF}{AF}=\frac{7}{25}$求出△EDC的面积即可.
解答 (1)证明:在矩形ABCD中,AD=BC,AD∥BC,∴∠DAC=∠ACB,
∵将矩形沿AC折叠后,点B与点E重合,∴EC=BC,∠ACB=∠ACE
∴AD=EC,∠DAC=∠ACE,∴AF=FC,∴AD-AF=EC-FC,即EF=DF
∴∠DEF=∠EDF
又∵∠DAC+∠ACE+∠AFC=180°,∠DEF+∠EDF+∠DFE=180°,∠AFC=∠DFE
∴∠DAC=∠EDF
∴ED∥AC.
(2)解:在矩形ABCD中,∠B=90°,又∵AB=3,BC=4,∴S△ABC=6,且AC=5,
设AF的长为x,FD=4-x,FD=x,CD=3,∠CDF=90°,由勾股定理得(4-x)2=x2+9,
解得$x=\frac{25}{8}$,∴FD=$\frac{7}{8}$,∴AF:FD=25:7
∵△ABC折叠为△AEC,∴S△AEC=6,∵ED∥AC,∴△EDC与△AEC等高,
∴$\frac{{{S_{△EDC}}}}{{{S_{△AEC}}}}=\frac{ED}{AC}=\frac{DF}{AF}=\frac{7}{25}$,∴${S_{△EDC}}=\frac{42}{25}$,∴${S_{四边形ACDE}}=6+\frac{42}{25}=\frac{192}{25}$.
点评 本题考查翻折变换、勾股定理、平行线的判定定理等知识,解题的关键是利用平行线间的距离相等,得△AEC与△EDC的面积比等于AC:ED=AF:DF,属于中考常考题型.

 阅读快车系列答案
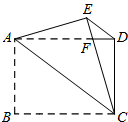
阅读快车系列答案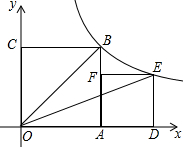 如图,两个正方形OABC、ADEF拼放于直角坐标系中,反比例函数y=$\frac{k}{x}(k≠0,x>0)$的图象经过B点和E点,已知△OEB的面积为2,则正方形ADEF的面积为( )
如图,两个正方形OABC、ADEF拼放于直角坐标系中,反比例函数y=$\frac{k}{x}(k≠0,x>0)$的图象经过B点和E点,已知△OEB的面积为2,则正方形ADEF的面积为( )| A. | 1 | B. | 6-2$\sqrt{5}$ | C. | $\sqrt{5}-1$ | D. | 3$\sqrt{5}$-5 |
 如图,已知点A、B、C,根据下列语句画图:(尺规作图,要保留作图痕迹.)
如图,已知点A、B、C,根据下列语句画图:(尺规作图,要保留作图痕迹.)(1)画出直线AB;
(2)画出射线AC;
(3)在线段AB的延长线上截取线段BD,使得AD=AB+BC;
(4)画出线段CD.
| A. | 0 | B. | $\sqrt{3}$ | C. | 2 | D. | -3 |
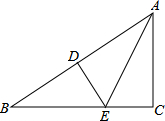 如图,DE是△ABC的AB边的垂直平分线,分别交AB、BC于点D、E,AE平分∠BAC,∠C=90°,则∠B的度数为( )
如图,DE是△ABC的AB边的垂直平分线,分别交AB、BC于点D、E,AE平分∠BAC,∠C=90°,则∠B的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
 (1)一不透明纸箱中装有形状、大小、质地等完全相同的4个小球,分别标有数字1,2,3,4.
(1)一不透明纸箱中装有形状、大小、质地等完全相同的4个小球,分别标有数字1,2,3,4.