题目内容
3．如图是由25个边长为1的小正方形组成的5×5网格，请分别在3个网格图中画出3个顶点在格点上的等腰三角形，要求：腰长为5且面积各不相同．
分析 由等腰三角形的定义：两条边相等再结合勾股定理画图即可．
解答 解：如图所示：（答案不唯一，满足条件即可）
点评 本题考查了作图-应用与设计作图，用到的知识点有勾股定理及等腰三角形的性质，先根据勾股定理求出等腰三角形的腰长是解答此题的关键．
练习册系列答案
灵星计算小达人系列答案
相关题目
14．
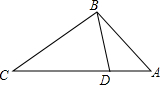如图，点D在△ABC的边AC上，要判断△ADC与△ABC相似，添加一个条件，不正确的是（ ）
如图，点D在△ABC的边AC上，要判断△ADC与△ABC相似，添加一个条件，不正确的是（ ）| A． | ∠ABD=∠C | B． | ∠ADB=∠ABC | C． | CB2=CD•CA | D． | AB2=AD•AC |
18．要说明命题“若a＞b，则|a|＞|b|”是假命题，能举的一个反例是（ ）
| A． | a=3，b=2 | B． | a=4，b=-1 | C． | a=1，b=0 | D． | a=1，b=-2 |
8．已知反比例函数的 图象经过点P（2，-1），则这个反比例函数的解析式为（ ）
| A． | y=$\frac{1}{x}$ | B． | y=-$\frac{1}{x}$ | C． | y=$\frac{2}{x}$ | D． | y=-$\frac{2}{x}$ |
15．
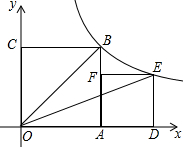如图，两个正方形OABC、ADEF拼放于直角坐标系中，反比例函数y=$\frac{k}{x}（k≠0，x＞0）$的图象经过B点和E点，已知△OEB的面积为2，则正方形ADEF的面积为（ ）
如图，两个正方形OABC、ADEF拼放于直角坐标系中，反比例函数y=$\frac{k}{x}（k≠0，x＞0）$的图象经过B点和E点，已知△OEB的面积为2，则正方形ADEF的面积为（ ）| A． | 1 | B． | 6-2$\sqrt{5}$ | C． | $\sqrt{5}-1$ | D． | 3$\sqrt{5}$-5 |
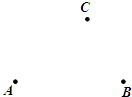如图，已知点A、B、C，根据下列语句画图：（尺规作图，要保留作图痕迹．）