题目内容
解答题
（1）已知a+b=3，a2+b2=5，求ab的值；
（2）若3m=8，3n=2，求32m-3n+1的值．
（1）已知a+b=3，a2+b2=5，求ab的值；
（2）若3m=8，3n=2，求32m-3n+1的值．
考点：完全平方公式,同底数幂的乘法,幂的乘方与积的乘方,同底数幂的除法
专题：计算题
分析：（1）运用完全平方公式求解；
（2）利用同底数幂的乘除法，幂的乘方与积的乘方化成含有3m，3n的式子求解．
（2）利用同底数幂的乘除法，幂的乘方与积的乘方化成含有3m，3n的式子求解．
解答：解：（1）[（a+b）2-（a2+b2）]÷2
=[9-5]÷2
=2；
（2）∵3m=8，3n=2
∴32m-3n+1=（3m）2÷（3n）3×3=64÷8×3=24．
=[9-5]÷2
=2；
（2）∵3m=8，3n=2
∴32m-3n+1=（3m）2÷（3n）3×3=64÷8×3=24．
点评：本题主要考查了完全平方公式，同底数幂的乘除法，幂的乘方与积的乘方，解题的关键是熟记法则和公式求解．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
如图，图①、图②、图③分别表示甲、乙、丙三人由A地到B地的路线图（箭头表示行进方向）其中图②中E为AB的中点，图③中AH＞BH，我们用a、b、c分别代表三人走过的路程，则a、b、c的大小关系为（ ）
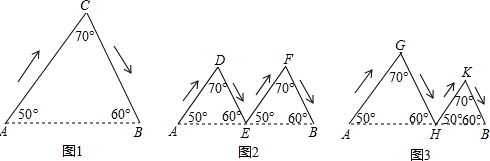
| A、a＞b=c |
| B、a＜b=c |
| C、a＞b＞c |
| D、a=b=c |
如图，抛物线y=ax2+bx-4a经过A（-1，0）、C（0，4）两点，与x轴交于另一点B．
已知∠AOB=30°，P是OA上的一点，OP=4cm，以r为半径作⊙P，若r=