题目内容
 如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.(1)求抛物线的解析式;
(2)已知点D(m,m+1)在第一象限的抛物线上,连结CD、BD,把△BCD沿BC折叠,
①求点D的对应点Dˊ的坐标;
②在抛物线上是否存在点P,使得△DDˊP是以DDˊ为一直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)把A(-1,0)、C(0,4)两点的坐标代入y=ax2+bx-4a,根据待定系数法可得这个抛物线的解析式;
(2)①如图①,将点D(m,m+1)代入y=-x2+3x+4中,得到D点坐标,根据等腰直角三角形的判定可得△OBC是等腰直角三角形,根据折叠的性质进一步得到点D的对应点Dˊ的坐标;
②存在满足条件的点P.如图②,过D′作D′E∥BC交x轴于E,交抛物线于P,根据待定系数法可得直线D′E的解析式,联立方程组可得点P的坐标;过D作DF∥BC交y轴于F,交抛物线于P,根据待定系数法可得直线D′E的解析式,联立方程组可得点P的坐标.
(2)①如图①,将点D(m,m+1)代入y=-x2+3x+4中,得到D点坐标,根据等腰直角三角形的判定可得△OBC是等腰直角三角形,根据折叠的性质进一步得到点D的对应点Dˊ的坐标;
②存在满足条件的点P.如图②,过D′作D′E∥BC交x轴于E,交抛物线于P,根据待定系数法可得直线D′E的解析式,联立方程组可得点P的坐标;过D作DF∥BC交y轴于F,交抛物线于P,根据待定系数法可得直线D′E的解析式,联立方程组可得点P的坐标.
解答:解:(1)把A(-1,0)、C(0,4)两点的坐标代入y=ax2+bx-4a,得
,
解得
.
所以这个抛物线的解析式为y=-x2+3x+4.
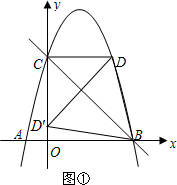 (2)①如图①,将点D(m,m+1)代入y=-x2+3x+4中,得:-m2+3m+4=m+1,
(2)①如图①,将点D(m,m+1)代入y=-x2+3x+4中,得:-m2+3m+4=m+1,
化简得:m2-2m-3=0
解得:m1=-1(舍去),m2=3;
∴D(3,4),
∴CD∥x轴,
∴∠DCO=90°,
由B(4,0)、C(0,4)可得:OB=4,
即△OBC是等腰直角三角形,得:∠OCB=∠DCB=45°;
把△BCD沿BC折叠,点D的对称点为点D′落在y轴上,
且CD=CD′=3,OD′=OC-CD′=1,
则点D′的坐标为(0,1).
②存在满足条件的点P.
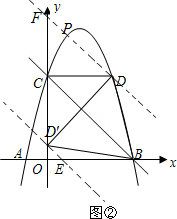 如图②,过D′作D′E∥BC交x轴于E,交抛物线于P.
如图②,过D′作D′E∥BC交x轴于E,交抛物线于P.
∵DD′⊥BC
∴∠DD'P=90°,△OD'E为等腰直角三角形
则E(1,0)
设直线D′E的解析式为y=k1x+b1,依题意得
,
解得
∴直线D′E的解析式为y=-x+1.
由
得
,
,
过D作DF∥BC交y轴于F,交抛物线于P.
∵DD′⊥BC
∴∠D′DP=90°,△CDF为等腰直角三角形
则F(0,7)
设直线DF的解析式为y=k2x+b2,依题意得
,
解得
.
∴直线DF的解析式为y=-x+7.
由
得
,
(不符合题意舍去).
故在抛物线上存在点P,使得△DD′P是以DD′为一直角边的直角三角形,点P的坐标为(2-
,-1+
)或(2+
,-1-
)或(1,6).
|
解得
|
所以这个抛物线的解析式为y=-x2+3x+4.
 (2)①如图①,将点D(m,m+1)代入y=-x2+3x+4中,得:-m2+3m+4=m+1,
(2)①如图①,将点D(m,m+1)代入y=-x2+3x+4中,得:-m2+3m+4=m+1,化简得:m2-2m-3=0
解得:m1=-1(舍去),m2=3;
∴D(3,4),
∴CD∥x轴,
∴∠DCO=90°,
由B(4,0)、C(0,4)可得:OB=4,
即△OBC是等腰直角三角形,得:∠OCB=∠DCB=45°;
把△BCD沿BC折叠,点D的对称点为点D′落在y轴上,
且CD=CD′=3,OD′=OC-CD′=1,
则点D′的坐标为(0,1).
②存在满足条件的点P.
 如图②,过D′作D′E∥BC交x轴于E,交抛物线于P.
如图②,过D′作D′E∥BC交x轴于E,交抛物线于P.∵DD′⊥BC
∴∠DD'P=90°,△OD'E为等腰直角三角形
则E(1,0)
设直线D′E的解析式为y=k1x+b1,依题意得
|
解得
|
∴直线D′E的解析式为y=-x+1.
由
|
|
|
过D作DF∥BC交y轴于F,交抛物线于P.
∵DD′⊥BC
∴∠D′DP=90°,△CDF为等腰直角三角形
则F(0,7)
设直线DF的解析式为y=k2x+b2,依题意得
|
解得
|
∴直线DF的解析式为y=-x+7.
由
|
|
|
故在抛物线上存在点P,使得△DD′P是以DD′为一直角边的直角三角形,点P的坐标为(2-
| 7 |
| 7 |
| 7 |
| 7 |
点评:考查了二次函数综合题,涉及的知识点有:待定系数法求抛物线的解析式,等腰直角三角形的判定,折叠的性质,待定系数法求直线的解析式,方程思想,分类思想的运用,综合性较强,有一定的难度.

练习册系列答案
相关题目
已知数据-1、2、3、-π、-5,其中负数出现的频率是( )
| A、20% | B、40% |
| C、50% | D、60% |
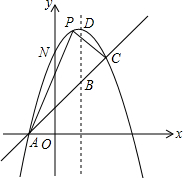 如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交与点N其顶点为D.
如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交与点N其顶点为D.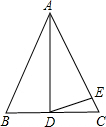 如图所示,在△ABC中,AB=AC,D为底边BC上任意一点,E为AC上一点,且AE=AD.
如图所示,在△ABC中,AB=AC,D为底边BC上任意一点,E为AC上一点,且AE=AD.