题目内容
17.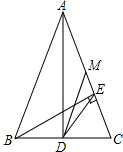 已知:在△ABC中,AB=AC,AD⊥BC,垂足为D,BE⊥AC,垂足为E,M为AC的中点,联结DE、DM,设∠C=α.
已知:在△ABC中,AB=AC,AD⊥BC,垂足为D,BE⊥AC,垂足为E,M为AC的中点,联结DE、DM,设∠C=α.(1)当△ABC是锐角三角形时,试用α表示∠EDM;
(2)当△ABC是钝角三角形时,请画出相应的图形,并用α表示∠EDM(可直接写出).
分析 (1)根据等腰三角形三线合一的性质可得BD=CD,根据直角三角形斜边上的中线等于斜边的一半可得CD=DE,CM=DM,再根据等腰三角形两底角相等求出∠CDE和∠CDM,然后根据∠EDM=∠CDM-∠CDE整理即可得解;
(2)作出图形,然后同(1)表示出∠CDE和∠CDM,再根据∠EDM=∠CDE-∠CDM整理即可得解.
解答 解:(1)∵AB=AC,AD⊥BC,
∴BD=CD,
∵BE⊥AC,
∴CD=DE=$\frac{1}{2}$BC,
∴∠CDE=180°-2∠C=180°-2α,
∵AD⊥BC,M为AC的中点,
∴CM=DM=$\frac{1}{2}$AC,
∴∠CDM=∠C=α,
∴∠EDM=∠CDM-∠CDE=α-(180°-2α)=3α-180°;
(2)如图,∠CDE=180°-2∠C=180°-2α,
∠CDM=∠C=α,
∠EDM=∠CDE-∠CDM=180°-2α-α=180°-3α.
点评 本题考查了等腰三角形的性质,直角三角形斜边上的中线等于斜边的一半的性质,熟记性质并观察图形得到∠EDM的表示是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
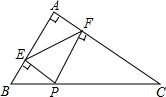 如图,在△ABC中,∠BAC=90°,AB=6,AC=8,点P是BC边上任意一点(B、C除外)PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF的最小值为4.8.
如图,在△ABC中,∠BAC=90°,AB=6,AC=8,点P是BC边上任意一点(B、C除外)PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF的最小值为4.8.