题目内容
9.有7张卡片正面分别标有数字-1,0,2,4,6,8,10,背面完全相同,将它们背面朝上,从中任意取一张作为横坐标x,纵坐标为y=$\frac{1}{2}$x+1,则点(x,y)落在y=-$\frac{1}{2}$x+5和y=-$\frac{5}{16}$x2+$\frac{5}{2}$x的图象围成的封闭区域(含边界)的概率为$\frac{2}{7}$.分析 由有7张卡片正面分别标有数字-1,0,2,4,6,8,10,背面完全相同,将它们背面朝上,从中任意取一张作为横坐标x,纵坐标为y=$\frac{1}{2}$x+1,可求得所有点的坐标,又由点(x,y)落在y=-$\frac{1}{2}$x+5和y=-$\frac{5}{16}$x2+$\frac{5}{2}$x的图象围成的封闭区域(含边界)的有(4,3),(6,4),即可求得答案.
解答 解:∵有7张卡片正面分别标有数字-1,0,2,4,6,8,10,背面完全相同,将它们背面朝上,从中任意取一张作为横坐标x,纵坐标为y=$\frac{1}{2}$x+1,
∴点(x,y)分别为:(-1,$\frac{1}{2}$),(0,1),(2,2),(4,3),(6,4),(8,5),(10,6),
∵点(x,y)落在y=-$\frac{1}{2}$x+5和y=-$\frac{5}{16}$x2+$\frac{5}{2}$x的图象围成的封闭区域(含边界)的有(4,3),(6,4),
∴点(x,y)落在y=-$\frac{1}{2}$x+5和y=-$\frac{5}{16}$x2+$\frac{5}{2}$x的图象围成的封闭区域(含边界)的概率为:$\frac{2}{7}$.
故答案为:$\frac{2}{7}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
19.现要把228吨物资从某地运往甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的
总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
| 运往地 车 型 | 甲 地(元/辆) | 乙 地(元/辆) |
| 大货车 | 720 | 800 |
| 小货车 | 500 | 650 |
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的
总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
18.如果a是(-8)2的平方根,那么$\root{3}{a}$等于( )
| A. | -8 | B. | -2 | C. | ±8 | D. | ±2 |
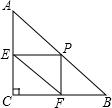 如图,在△ABC中,∠C=90°,AB=10,$\frac{BC}{AC}$=$\frac{3}{4}$,过AB边上一点P作PE⊥AC于点E,PF⊥BC于点F,则EF的最小值是$\frac{24}{5}$.
如图,在△ABC中,∠C=90°,AB=10,$\frac{BC}{AC}$=$\frac{3}{4}$,过AB边上一点P作PE⊥AC于点E,PF⊥BC于点F,则EF的最小值是$\frac{24}{5}$.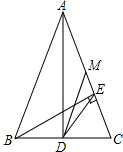 已知:在△ABC中,AB=AC,AD⊥BC,垂足为D,BE⊥AC,垂足为E,M为AC的中点,联结DE、DM,设∠C=α.
已知:在△ABC中,AB=AC,AD⊥BC,垂足为D,BE⊥AC,垂足为E,M为AC的中点,联结DE、DM,设∠C=α.
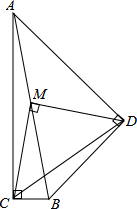 如图,M是Rt△ABC与Rt△ABD的公共边AB的中点,连接CM,DM,恰好△CMD为直角三角形,若BD=6,AD=8,求CD的长.
如图,M是Rt△ABC与Rt△ABD的公共边AB的中点,连接CM,DM,恰好△CMD为直角三角形,若BD=6,AD=8,求CD的长.