题目内容
如图,平面直角坐标系中,原点为O,点A、M的坐标分别为(0,8)、(3,4),AM的延长线交x轴于点B.点P为线段AO上的一个动点,点P从点O沿OA方向以1个单位/秒的速度向A运动,正方形PCEF边长为2(点C在y轴上,点E、F在y轴右侧).设运动时间为t秒.
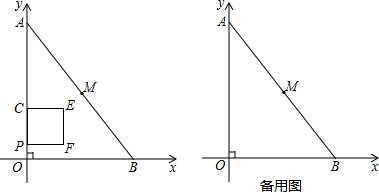
(1)正方形PCEF的对角线PE所在直线的函数表达式为 (用含t的式子表示),若正方形PCEF的对角线PE所在直线恰好经过点M,则时间t为 秒.
(2)若正方形PCEF始终在△AOB内部运动,求t的范围.
(3)在条件(2)下,设△PEM的面积为y,求y与t的函数表达式.

(1)正方形PCEF的对角线PE所在直线的函数表达式为
(2)若正方形PCEF始终在△AOB内部运动,求t的范围.
(3)在条件(2)下,设△PEM的面积为y,求y与t的函数表达式.
考点:一次函数综合题
专题:
分析:(1)根据直线PE平行于y=x,再根据P点坐标,可得函数解析式,根据图象上的点满足函数解析式,把点的坐标代入函数解析式,可得答案;
(2)根据E点坐标在直线AB的下方,可得t的取值范围;
(3)分类讨论,0≤t≤1时,根据直线PM与CE,可得E点坐标,根据两点间距离公式,可得EQ的长,根据三角形的面积公式,可得答案;1<t≤
时,根据直线PM与EF,可得E点坐标,根据两点间距离公式,可得EQ的长,根据三角形的面积公式,可得答案.
(2)根据E点坐标在直线AB的下方,可得t的取值范围;
(3)分类讨论,0≤t≤1时,根据直线PM与CE,可得E点坐标,根据两点间距离公式,可得EQ的长,根据三角形的面积公式,可得答案;1<t≤
| 16 |
| 3 |
解答:解:(1)y=x+t,1,
故答案为;y=x+t,1;
(2)设直线AM:y=kx+8,
将M(3,4)代入
k=-
,
∴直线AM:y=-
x+8,
将E(2,2+t)代入直线AM解析式得t=
∴0≤t≤
;
(3)①当0≤t≤1时,如图一,连接PM交CE于Q点 ,
,
∵P(0,t),M(3,4)
∴直线PM:y=
x+t
∴Q(
,2+t)
∴EQ=2-
=
∴y=
×EQ×|yM-yP|=
×
×(4-t)=1-t;
②当1<t≤
时,如图二,连接PM交EF于Q点 ,
,
同①得,直线PM:y=
x+t
∴Q(2,
)
∴EQ=2+t-
=
∴y=
×EQ×|xM-xP|=
×
×3=t-1;
综上所述∴y=
.
故答案为;y=x+t,1;
(2)设直线AM:y=kx+8,
将M(3,4)代入
k=-
| 4 |
| 3 |
∴直线AM:y=-
| 4 |
| 3 |
将E(2,2+t)代入直线AM解析式得t=
| 10 |
| 3 |
∴0≤t≤
| 10 |
| 3 |
(3)①当0≤t≤1时,如图一,连接PM交CE于Q点
 ,
,∵P(0,t),M(3,4)
∴直线PM:y=
| 4-t |
| 3 |
∴Q(
| 6 |
| 4-t |
∴EQ=2-
| 6 |
| 4-t |
| 2-2t |
| 4-t |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 2-2t |
| 4-t |
②当1<t≤
| 10 |
| 3 |
 ,
,同①得,直线PM:y=
| 4-t |
| 3 |
∴Q(2,
| 8+t |
| 3 |
∴EQ=2+t-
| 8+t |
| 3 |
| 2t-2 |
| 3 |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 2t-2 |
| 3 |
综上所述∴y=
|
点评:本题考查了一次函数综合题,(1)利用了平行线间的函数关系,(2)点与直线的关系,(3)三角形的面积和差是解题关键.

练习册系列答案
相关题目
 某校为了解九年级1200名学生的交通安全知识,对全校九年级学生进行曲了一次交通安全测试,并随机抽取50名学生的成绩,整理后分成五组,制成如下统计图表.请根据图表信息解答下列总理:
某校为了解九年级1200名学生的交通安全知识,对全校九年级学生进行曲了一次交通安全测试,并随机抽取50名学生的成绩,整理后分成五组,制成如下统计图表.请根据图表信息解答下列总理:
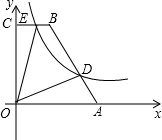 如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,双曲线y=
如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,双曲线y=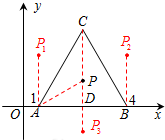 如图,等边三角形ABC在平面直角坐标系中,A(1,0)、B(4,0),C点在第一象限,点P是△ABC三条高的交点,则点P关于△ABC各边所在直线的对称点的坐标是
如图,等边三角形ABC在平面直角坐标系中,A(1,0)、B(4,0),C点在第一象限,点P是△ABC三条高的交点,则点P关于△ABC各边所在直线的对称点的坐标是