题目内容
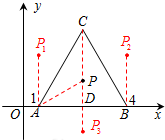 如图,等边三角形ABC在平面直角坐标系中,A(1,0)、B(4,0),C点在第一象限,点P是△ABC三条高的交点,则点P关于△ABC各边所在直线的对称点的坐标是
如图,等边三角形ABC在平面直角坐标系中,A(1,0)、B(4,0),C点在第一象限,点P是△ABC三条高的交点,则点P关于△ABC各边所在直线的对称点的坐标是考点:坐标与图形变化-对称,等边三角形的性质
专题:
分析:根据点A、B的坐标求出等边三角形的边长AB,根据等腰三角形三线合一的性质求出AD,然后求出OD、AP、PD,再根据线段垂直平分线上的点到两端点的距离相等可得AP1=AP2=AP3=AP,然后写出点P关于各边的对称点的坐标即可.
解答:解:∵A(1,0)、B(4,0),
∴△ABC的边长为3,
∵P是△ABC三条高的交点,
∴AD=
,
∴OD=1+
=
,
AP=
÷
=
,PD=
AP=
,
∴点P的坐标为(
,
),
易知∠P1AB=∠P2BA=90°,AP1=AP2=AP3=AP=
,
∴P1(1,
),P2(4,
),P3(
,-
).
故答案为:P1(1,
),P2(4,
),P3(
,-
).
∴△ABC的边长为3,
∵P是△ABC三条高的交点,
∴AD=
| 3 |
| 2 |
∴OD=1+
| 3 |
| 2 |
| 5 |
| 2 |
AP=
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴点P的坐标为(
| 5 |
| 2 |
| ||
| 2 |
易知∠P1AB=∠P2BA=90°,AP1=AP2=AP3=AP=
| 3 |
∴P1(1,
| 3 |
| 3 |
| 5 |
| 2 |
| ||
| 2 |
故答案为:P1(1,
| 3 |
| 3 |
| 5 |
| 2 |
| ||
| 2 |
点评:本题考查了坐标与图形变化-对称,等边三角形的性质,熟练掌握等边三角形的性质是解题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
 如图,将周长为8的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为( )
如图,将周长为8的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为( )| A、8 | B、10 | C、12 | D、14 |