题目内容
 在平行四边形ABCD中,点E、H、F、G分别在边AB、BC、CD、DA上,AD∥EF,CD∥GH,EF与GH相交于点O,共有多少个平行四边形?
在平行四边形ABCD中,点E、H、F、G分别在边AB、BC、CD、DA上,AD∥EF,CD∥GH,EF与GH相交于点O,共有多少个平行四边形?考点:平行四边形的判定与性质
专题:
分析:由在平行四边形ABCD中,点E、H、F、G分别在边AB、BC、CD、DA上,AD∥EF,CD∥GH,可得AB∥GH∥CD,AD∥EF∥BC,即可得平行四边形有:?ABCD,?ABHG,?CDGH,?BCFE,?ADFE,?AGOE,?BEOH,?OFCH,?OGDF共9个
解答:解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵AD∥EF,CD∥GH,
∴AB∥GH∥CD,AD∥EF∥BC,
∴平行四边形有:?ABCD,?ABHG,?CDGH,?BCFE,?ADFE,?AGOE,?BEOH,?OFCH,?OGDF共9个.
即共有9个平行四边形.
∴AB∥CD,AD∥BC,
∵AD∥EF,CD∥GH,
∴AB∥GH∥CD,AD∥EF∥BC,
∴平行四边形有:?ABCD,?ABHG,?CDGH,?BCFE,?ADFE,?AGOE,?BEOH,?OFCH,?OGDF共9个.
即共有9个平行四边形.
点评:此题考查了平行四边形的判定与性质.此题比较简单,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,在△ABC中,BG为高,点E、F、D分别在BC、AC、AB上,且EF⊥AC,∠1=∠2,∠ABC=60°,求∠ADG的度数.
如图,在△ABC中,BG为高,点E、F、D分别在BC、AC、AB上,且EF⊥AC,∠1=∠2,∠ABC=60°,求∠ADG的度数. 如图,直线y=2x+2与y轴交于A点,与反比例函数y=
如图,直线y=2x+2与y轴交于A点,与反比例函数y= 将一张矩形纸片ABCD(AB<2AD),以它的一条宽为边长剪去一个正方形,将剩下的矩形再以一条宽为边长剪去一个正方形,若第二次剪裁后所留下的矩形与原来的矩形ABCD相似,则矩形ABCD的宽与长的比值是多少?
将一张矩形纸片ABCD(AB<2AD),以它的一条宽为边长剪去一个正方形,将剩下的矩形再以一条宽为边长剪去一个正方形,若第二次剪裁后所留下的矩形与原来的矩形ABCD相似,则矩形ABCD的宽与长的比值是多少?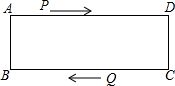 在矩形ABCD中,AD=12cm,点P在AD边以1cm/s的速度从点A向点D运动,点Q从C点出发,以4cm/s的速度在CB间做往返运动,两点同时出发,直到点P到达点D时,P、Q都停止运动,设运动时间为t秒,当t为多少时,四边形ABQP为矩形?
在矩形ABCD中,AD=12cm,点P在AD边以1cm/s的速度从点A向点D运动,点Q从C点出发,以4cm/s的速度在CB间做往返运动,两点同时出发,直到点P到达点D时,P、Q都停止运动,设运动时间为t秒,当t为多少时,四边形ABQP为矩形?