Question

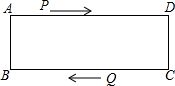在矩形ABCD中，AD=12cm，点P在AD边以1cm/s的速度从点A向点D运动，点Q从C点出发，以4cm/s的速度在CB间做往返运动，两点同时出发，直到点P到达点D时，P、Q都停止运动，设运动时间为t秒，当t为多少时，四边形ABQP为矩形？

Answer 1

考点：矩形的判定与性质

专题：动点型

分析：当四边形ABQP为矩形时，则AP=BQ，列式可求得t的值．

解答：解：∵在矩形ABCD中，AD=12cm，
∴AD=BC=12cm．
当四边形ABQP为矩形时，AP=BQ．
①当0＜t＜3时，t=12-4t，
解得，t=

12

5

；
②当3≤t＜6时，t=4t-12，
解得 t=4；
③当6≤t＜9时，t=36-4t，
解得 t=

36

5

；
④当9≤t≤12时，t=4t-36，
解得，t=12．
综上所述，当t为

12

5

或4或

36

5

或12时，四边形ABQP为矩形．

点评：本题考查了矩形的性质和平行线的性质．解决本题的关键是理解平行的次数就是Q在BC上往返运动的次数．