题目内容
 将一张矩形纸片ABCD(AB<2AD),以它的一条宽为边长剪去一个正方形,将剩下的矩形再以一条宽为边长剪去一个正方形,若第二次剪裁后所留下的矩形与原来的矩形ABCD相似,则矩形ABCD的宽与长的比值是多少?
将一张矩形纸片ABCD(AB<2AD),以它的一条宽为边长剪去一个正方形,将剩下的矩形再以一条宽为边长剪去一个正方形,若第二次剪裁后所留下的矩形与原来的矩形ABCD相似,则矩形ABCD的宽与长的比值是多少?考点:相似多边形的性质
专题:
分析:先根据题意画出图形,设BC=x,CD=y,则HF=2y-x,BF=x-y,根据矩形ABCD∽矩形GBEH和矩形ABCD∽矩形BEHG,列出比例式,求出比值即可.
解答:解:根据题意画图如下:

设BC=x,CD=y,则HF=2y-x,BF=x-y,若矩形ABCD∽矩形GBEH,
则:
=
,
解得:
=
,
若矩形ABCD∽矩形BEHG,则
=
,
解得:
=
.

设BC=x,CD=y,则HF=2y-x,BF=x-y,若矩形ABCD∽矩形GBEH,
则:
| x |
| y |
| x-y |
| 2y-x |
解得:
| y |
| x |
| ||
| 2 |
若矩形ABCD∽矩形BEHG,则
| x |
| y |
| 2y-x |
| x-y |
解得:
| y |
| x |
| ||
| 2 |
点评:此题考查了相似多边形的性质,关键是根据题意画出图形,根据相似多边形的性质列出比例式,注意分两种情况进行讨论.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
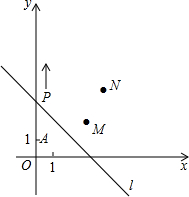 如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒. 我们知道:三角形的三条中线的交点也是三角形重心.如图,点G是△ABC的重心,求证:AG=2GD.
我们知道:三角形的三条中线的交点也是三角形重心.如图,点G是△ABC的重心,求证:AG=2GD. 在平行四边形ABCD中,点E、H、F、G分别在边AB、BC、CD、DA上,AD∥EF,CD∥GH,EF与GH相交于点O,共有多少个平行四边形?
在平行四边形ABCD中,点E、H、F、G分别在边AB、BC、CD、DA上,AD∥EF,CD∥GH,EF与GH相交于点O,共有多少个平行四边形?