题目内容
如图所示，转盘被等分成六个扇形，并在上面依次写上数字1、2、3、4、5、6.
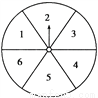
（1）若自由转动转盘，当它停止转动时，指针指向奇数区的概率是多少？
（2）请你用这个转盘设计一个游戏，当自由转动的转盘停止时，指针指向的区域的概率为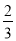
.
（1）；（2）详见解析．
【解析】试题分析：（1）自由转动转盘，当它停止转动时，指针指向数字的结果总共有6种，指针指向奇数区的结果有3种，所以指针指向奇数区的概率是．
（2）当自由转动的转盘停止时，指针指向的区域不大于4．（答案不唯一，符合要求即可）
试题解析：（1）指针指向奇数区的概率是．
（2）当自由转动的转盘停止时，指针指向的区域不大于4．（答案不唯一，符合要求即可）...
练习册系列答案
相关题目
如图,∠1=∠2,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.试说明:∠BAP+∠BCP=180°.
见解析
【解析】作PE垂直于AB于E，根据角平分线的性质可知PD=PE，HL定理可知△PBD≌△PBE，可得BD=BE，根据题中线段和差的关系，可得△PAE≌△PCD，所以可知∠PAE=∠PCD，根据∠PAE+∠PAB=180°，即可证明题中关系.
证明：如图，过点P作PE⊥BA于E.
∵PD⊥BC，PE⊥BM，∠1=∠2，
∴PD=PE.
∵PD⊥BC，PE⊥BM，... 如图所示，F、C在线段BE上，且∠1＝∠2，BC＝EF.若要根据“SAS”使△ABC≌△DEF，还需要补充的条件是________.
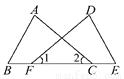
AC＝DF
【解析】已知∠1＝∠2，BC＝EF，根据“SAS”使△ABC≌△DEF，还需要补充的条件是AC＝DF. 甲．乙．丙三个事件发生的概率分别为0.5，0.1，0.9，它们各与下面的哪句话相配．
(1)发生的可能性很大，但不一定发生；
(2)发生的可能性很小；
(3)发生与不发生的可能性一样．
（1）发生的概率为0.9.
（2）发生的概率为0.1.
（3）发生的概率为0.5.
【解析】试题分析：
（1）概率比较大；
（2）概率比较小；
（3）概率为0.5.
试题解析：
（1）发生的可能性很大，但不一定发生，匹配发生的概率为0.9.
（2）发生的可能性很小，匹配发生的概率为0.1.
（3）发生与不发生的可能性一样，匹配发生的概率为... （3分）必然事件的概率是（ ）
A．﹣1 B．0 C．0.5 D．1
D．
【解析】
试题分析：∵必然事件就是一定发生的事件，∴必然事件发生的概率是1．故选D． 如图，转盘中6个小扇形的面积都相等，任意转动转盘1次，当转盘停止转动时，指针指向红色区域的概率为 ．
．
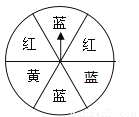
【解析】
试题分析：∵圆被等分成6份，其中红色部分占2份，∴落在阴影区域的概率==，故答案为：． 小颖和小明做游戏:一个不透明的袋子中装有6个完全一样的球,每个球上分别标有1,2,2,3,4,5,从袋中任意摸出一个球,然后放回.规定:若摸到的球上所标数字大于3,则小颖赢,否则小明赢.你认为这个游戏公平吗?为什么?如果不公平,请修改游戏规则,使游戏公平.
游戏不公平.修改规则如下:方法一:若摸到的球上所标数字小于3,则小颖赢;否则小明赢.方法二:若摸到的球上所标数字是偶数,则小颖赢,否则小明赢.
【解析】试题分析：分别计算出小颖赢和小明赢的概率即可；通过比较概率的大小来判断游戏是否公平．
试题解析：【解析】
P（小颖赢）=，P（小明赢）=，所以不公平．
修改规则如下：方法一：若摸到的球上所标数字小于3，则小颖赢；否则小明赢．
... 如图，A、B、C分别是线段A1B、B1C、C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积为____.
7
【解析】试题分析：如下图，连接A1C，B1A，C1B，，因B是线段B1C的中点，所以B1B="BC." △A1B1A和△AB1B等底同高，根据等底同高的两个三角形面积相等可得S△B1AB=S△ABC=1；同理可得S△A1B1A=S△AB1B=1；所以=S△A1B1A+S△AB1B=1+1=2；同理可得S△C1CB1=2， S△C1AA1=2.
S△A1B1C1= S△A1BB1+ ... －3x≤6的解集是 （ ）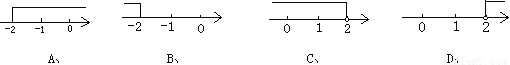
A
【解析】试题分析：由－3x≤6解得x≥－2，即可得到结果.
－3x≤6解得x≥－2，故选A.