题目内容
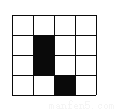
如图是4×4正方形网络，其中已有3个小方格涂成了黑色。现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形，这样的白色小方格有________个．
4
【解析】试题分析：根据轴对称图形的概念分别找出各个能成轴对称图形的小方格即可．如图所示，有4个位置使之成为轴对称图形．
故答案为：4．
为了解某种品牌小汽车的耗油量，我们对这种车在高速公路上做了耗油试验，并把试验的数据记录下来，制成下表：
汽车行驶时间t（h） | 0 | 1 | 2 | 3 | … |
油箱剩余油量Q（L） | 100 | 94 | 88 | 82 | … |
①根据上表的数据，请你写出Q与t的关系式；
②汽车行驶5h后，油箱中的剩余油量是多少？
③该品牌汽车的油箱加满50L，若以100km/h的速度匀速行驶，该车最多能行驶多远？
①Q=50﹣8t；②汽车行驶5h后，油箱中的剩余油量是10L；③该车最多能行驶625km. 【解析】试题分析：①由表格可知，开始油箱中的油为50L，每行驶1小时，油量减少8L，据此可得t与Q的关系式； ②求汽车行驶5h后，油箱中的剩余油量即是求当t=5时，Q的值； ③贮满50L汽油的汽车，理论上最多能行驶几小时即是求当Q=0时，t的值. 试题解析①Q与t的关系式为：Q=50...研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球.怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球试验.摸球试验的要求:先搅拌均匀,每次随机摸出一个球,放回盒中,再继续.
活动结果:摸球试验一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算.由上述的摸球试验可推算:
(1)盒中红球、黄球各占总球数的百分比是多少?
(2)盒中有红球多少个?
(1) 红球约占40%,黄球约占60%；(2) 40个.
【解析】分析：（1）根据表格数据可以得到50次摸球实验活动中，出现红球20次，黄球30次，由此即可求出盒中红球、黄球各占总球数的百分比；（2）由题意可知50次摸球实验活动中，出现有记号的球4次，由此可以求出总球数，然后利用（1）的结论即可求出盒中红球．
本题解析： (1)由题意可知,50次摸球试验中,出现红球20次,黄球30次,... 一次数学测试后，某班50名学生的成绩被分为5组，第1～4组的频数分别为12、10、15、8，则第5组的频率是（ ）
A. 0.1 B. 0.2 C. 0.3 D. 0.4
A
【解析】分析：由题意先求出第5组的频数，再由所求频数除以50即可得到第5组的频率.
详解：
∵总人数为50，第1～4组的频数分别为12、10、15、8，
∴第5组的频数为：50-12-10-15-8=5，
∴第5组的频率=5÷50=0.1.
故选A. 如图,关于虚线成轴对称的有( )个.
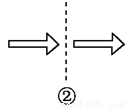
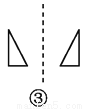
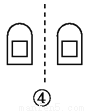
A. 1 B. 2 C. 3 D. 4
B
【解析】①关于虚线不成轴对称，②关于虚线不成轴对称，③关于虚线不成轴对称，④关于虚线成轴对称，
故选B. 若a、b、c为整数，且|a﹣b|19+|c﹣a|95=1，则|c﹣a|+|a﹣b|+|b﹣c|=______．
2
【解析】分两种情况：
①|a-b|=1，|c-a|=0，则c=a，
∴|c-a|+|a-b|+|b-c|=0+|a-b|+|b-a|=0+1+1=2；
②|a-b|=0，|c-a|=1，则a=b，
|c-a|+|a-b|+|b-c|=|c-a|+0+|a-c|=1+0+1=2，
∴|c-a|+|a-b|+|b-c|=2.
故答案为：2． 如图是一个四棱柱和一个六棱锥，它们各有12条棱．
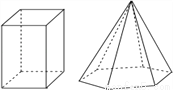
下列棱柱中和九棱锥的棱数相等的是（ ）
A. 五棱柱 B. 六棱柱 C. 七棱柱 D. 八棱柱
B
【解析】∵九棱锥有18条棱，五棱柱有15条棱， 六棱柱有18条棱，七棱柱有21条棱，八棱柱有24条棱，
∴六棱柱的棱数与九棱锥的棱数相等. 如图，已知在△ABC中，∠C=90°，AB的垂直平分线MN交BC于点D.
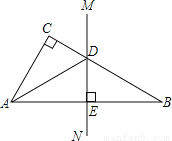
（1）如果∠CAD=20°，求∠B的度数；
（2）如果∠CAB=50°，求∠CAD的度数；
（3）如果∠CAD：∠DAB=1：2，求∠CAB的度数.
（1）∠B＝35°；（2）∠CAD=10°；（3）∠CAB=54°.
【解析】试题分析：（1）根据直角三角形的性质求出∠ADC=70°，根据线段的垂直平分线的性质得到DA=DB，计算即可；
（2）根据直角三角形的性质求出∠B的度数，根据线段的垂直平分线的性质得到DA=DB，计算即可；
（3）设∠CAD=x，根据题意列出方程，解方程即可．
试题解析：（1）∵∠C=90°，∠C...