题目内容
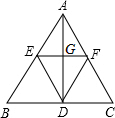 在△ABC中,AB=AC=5,BC=6,AD⊥BC,EF∥BC,则△EDF的最大面积为
在△ABC中,AB=AC=5,BC=6,AD⊥BC,EF∥BC,则△EDF的最大面积为考点:相似三角形的判定与性质,二次函数的最值
专题:
分析:利用勾股定理求得AD,设EF为x,利用平行得到线段成比例从而用x表示出GD,可得到△EDF的面积,利用二次函数的性质求其最大值即可.
解答:解:
∵AB=AC=5,AD⊥BC,
∴BD=
BC=3,
在Rt△ABD中可求得AD=4,
∵EF∥BC,
∴
=
,
设EF=x,且AG=AD-GD,
∴
=
,解得GD=4-
x,
∴S△EDF=
EF•GD=
x(4-
x)=-
x2+2x,
该函数开口向下,且由题意可知0<x<6,
∴当x=3时,S△EDF有最大值,最大值为3,
故答案为:3.
∵AB=AC=5,AD⊥BC,
∴BD=
| 1 |
| 2 |
在Rt△ABD中可求得AD=4,
∵EF∥BC,
∴
| EF |
| BC |
| AG |
| AD |
设EF=x,且AG=AD-GD,
∴
| x |
| 6 |
| 4-GD |
| 4 |
| 2 |
| 3 |
∴S△EDF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
该函数开口向下,且由题意可知0<x<6,
∴当x=3时,S△EDF有最大值,最大值为3,
故答案为:3.
点评:本题主要考查平行线分线段成比例,利用平行线分线段成比例性质得到GD和EF的关系,用x表示出△EDF的面积是解题的关键.注意函数思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,⊙O是以等腰Rt△ABC的斜边AB为直径的圆,点P是BA的延长线上的一点,过点P作⊙O的一条切线,切点为点Q,∠QPB的平分线交AC、BC于点E、F.
如图,⊙O是以等腰Rt△ABC的斜边AB为直径的圆,点P是BA的延长线上的一点,过点P作⊙O的一条切线,切点为点Q,∠QPB的平分线交AC、BC于点E、F. 如图,△ABC中,∠ACB=90°,CD⊥AB于D,BD=2,AD=8,求S△ABC.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,BD=2,AD=8,求S△ABC. 如图,点A,B,C,D,E,F分别在⊙O上,AC=BD,CE=DF,连接AE,BF.△ACE与△BDF全等吗?为什么?
如图,点A,B,C,D,E,F分别在⊙O上,AC=BD,CE=DF,连接AE,BF.△ACE与△BDF全等吗?为什么?
 如图,△ABC中,∠BAC=90°,∠C=30°,AD平分∠BAC交BC于D,AB=
如图,△ABC中,∠BAC=90°,∠C=30°,AD平分∠BAC交BC于D,AB=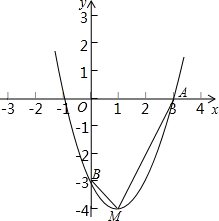 如图在直角坐标平面内,O为原点,点B坐标为(0,-3),且AO=BO,二次函数y=x2+bx+c经过A,B两点,顶点为M.
如图在直角坐标平面内,O为原点,点B坐标为(0,-3),且AO=BO,二次函数y=x2+bx+c经过A,B两点,顶点为M.