题目内容
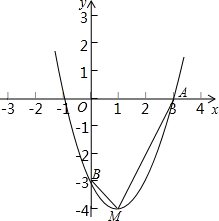 如图在直角坐标平面内,O为原点,点B坐标为(0,-3),且AO=BO,二次函数y=x2+bx+c经过A,B两点,顶点为M.
如图在直角坐标平面内,O为原点,点B坐标为(0,-3),且AO=BO,二次函数y=x2+bx+c经过A,B两点,顶点为M.(1)求这个二次函数解析式;
(2)求四边形OAMB的面积.
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征
专题:计算题
分析:(1)由AO=BO,根据B坐标确定出A坐标,把A与B坐标代入二次函数解析式求出b与c的值,即可确定出二次函数解析式;
(2)过M作MN垂直于x轴,四边形OAMB分为梯形OBMN与三角形AMN,求出即可.
(2)过M作MN垂直于x轴,四边形OAMB分为梯形OBMN与三角形AMN,求出即可.
解答: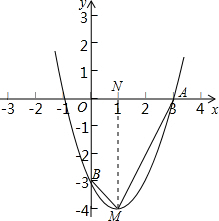 解:(1)∵OA=OB,且B(0,-3),
解:(1)∵OA=OB,且B(0,-3),
∴A(3,0),
把A(3,0),B(0,-3)代入得:
,
解得:b=2,c=-3,
则二次函数解析式为y=x2-2x-3;
(2)过M作MN⊥x轴,交x轴于点N,如图所示,
由(1)得到顶点M(1,-4),即MN=4,ON=1,
则S四边形AOBM=S梯形BONM+S△AMN=
×1×(3+4)+
×4×2=3.5+4=7.5.
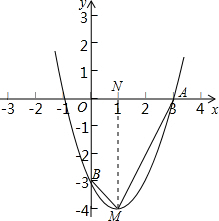 解:(1)∵OA=OB,且B(0,-3),
解:(1)∵OA=OB,且B(0,-3),∴A(3,0),
把A(3,0),B(0,-3)代入得:
|
解得:b=2,c=-3,
则二次函数解析式为y=x2-2x-3;
(2)过M作MN⊥x轴,交x轴于点N,如图所示,
由(1)得到顶点M(1,-4),即MN=4,ON=1,
则S四边形AOBM=S梯形BONM+S△AMN=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
已知
是二次根式,则x应满足的条件是( )
|
| A、x>0 | B、x≤0 |
| C、x≥-3 | D、x>-3 |
 在△ABC中,AB=AC=5,BC=6,AD⊥BC,EF∥BC,则△EDF的最大面积为
在△ABC中,AB=AC=5,BC=6,AD⊥BC,EF∥BC,则△EDF的最大面积为 如图,∠AOB=30°,P点在∠AOB内部,M点在射线OA上,将线段PM绕P点逆时针旋转90°,M点恰好落在OB上的N点(OM>ON),若PM=
如图,∠AOB=30°,P点在∠AOB内部,M点在射线OA上,将线段PM绕P点逆时针旋转90°,M点恰好落在OB上的N点(OM>ON),若PM= 如图,在△ABC中,∠BAC=40°,∠ABC=120°,AM、BN分别为∠BAC,∠ABC的角平分线,证明:AB+AN=AM+BM.
如图,在△ABC中,∠BAC=40°,∠ABC=120°,AM、BN分别为∠BAC,∠ABC的角平分线,证明:AB+AN=AM+BM.