题目内容
 如图,⊙O是以等腰Rt△ABC的斜边AB为直径的圆,点P是BA的延长线上的一点,过点P作⊙O的一条切线,切点为点Q,∠QPB的平分线交AC、BC于点E、F.
如图,⊙O是以等腰Rt△ABC的斜边AB为直径的圆,点P是BA的延长线上的一点,过点P作⊙O的一条切线,切点为点Q,∠QPB的平分线交AC、BC于点E、F.(1)求证:P、A、E、Q四点共圆.
(2)若AE=a,BF=b,求EF的长.
考点:四点共圆,全等三角形的判定与性质,等腰三角形的性质,勾股定理,圆周角定理,圆内接四边形的性质,切线的性质
专题:综合题
分析:(1)连接OQ、QE、QA,如图1,要证P、A、E、Q四点共圆,只需证到∠PQA=∠PEA,易证∠PEA=45°-
∠QPO,只需证到∠PQA=45°-
∠QPO,只需将∠PQA转化为∠OQA,将∠OQA转化为∠AOQ,将∠AOQ转化为∠QPO即可解决问题;
(2)连接OE、OF、OC,如图2,由P、A、E、Q四点共圆,∠QPE=∠EPA可得EQ=EA,从而证到△AEO≌△QEO,则有∠AOE=∠QOE,由此可得到∠FEO=45°=∠FCO,由此可得C、E、O、F四点共圆,根据圆内接四边形的性质可得∠EOF=90°,进而可证到△AEO≌△CFO,从而有CF=AE=a,进而可得CE=b,然后在Rt△ECF中运用勾股定理就可求出EF的长.
| 1 |
| 2 |
| 1 |
| 2 |
(2)连接OE、OF、OC,如图2,由P、A、E、Q四点共圆,∠QPE=∠EPA可得EQ=EA,从而证到△AEO≌△QEO,则有∠AOE=∠QOE,由此可得到∠FEO=45°=∠FCO,由此可得C、E、O、F四点共圆,根据圆内接四边形的性质可得∠EOF=90°,进而可证到△AEO≌△CFO,从而有CF=AE=a,进而可得CE=b,然后在Rt△ECF中运用勾股定理就可求出EF的长.
解答: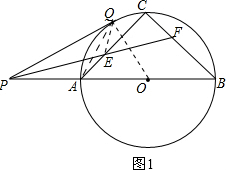 解:(1)连接OQ、QE、QA,如图1.
解:(1)连接OQ、QE、QA,如图1.
∵△ABC是等腰直角三角形,∠ACB=90°,
∴∠CAB=∠CBA=45°.
∵PF平分∠QPO,
∴∠QPE=∠EPA=
∠QPO.
∵PQ是⊙O的切线,
∴∠PQO=90°,
∴∠QOP=90°-∠QPO.
∵OQ=OA,
∴∠AQO=∠QAO=
(180°-∠QOP)
=
(180°-90°+∠QPO)
=45°+
∠QPO,
∴∠PQA=90°-∠AQO=90°-(45°+
∠QPO)
=45°-
∠QPO=∠CAB-∠EPA=∠PEA,
∴P、A、E、Q四点共圆.
(2)连接OE、OF、OC,如图2.
∵P、A、E、Q四点共圆,∠QPE=∠EPA
∴EQ=EA.
在△QEO和△AEO中,
,
∴△QEO≌△AEO(SSS),
∴∠QOE=∠AOE.
∵∠QPE+∠EPA+∠EOP+∠QOE=90°,
∴2∠EPA+2∠EOP=90°,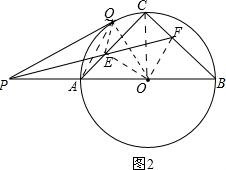
∴∠EPA+∠EOP=45°,
∴∠FEO=∠EPA+∠EOP=45°.
∵OC=OB,∴∠OCB=∠OBC=45°,
∴∠FEO=∠FCO=45°,
∴C、E、O、F四点共圆,
∴∠EOF+∠ECF=180°,
∴∠EOF=90°.
∵∠AOC=2∠B=90°,
∴∠EOF=∠AOC,
∴∠AOE=∠COF.
在△AEO和△CFO中,
,
∴△AEO≌△CFO(ASA).
∴AE=CF=a,
∴AC=BC=CF+BF=a+b,
∴CE=AC-AE=b.
∵∠ECF=90°,
∴EF=
=
.
 解:(1)连接OQ、QE、QA,如图1.
解:(1)连接OQ、QE、QA,如图1.∵△ABC是等腰直角三角形,∠ACB=90°,
∴∠CAB=∠CBA=45°.
∵PF平分∠QPO,
∴∠QPE=∠EPA=
| 1 |
| 2 |
∵PQ是⊙O的切线,
∴∠PQO=90°,
∴∠QOP=90°-∠QPO.
∵OQ=OA,
∴∠AQO=∠QAO=
| 1 |
| 2 |
=
| 1 |
| 2 |
=45°+
| 1 |
| 2 |
∴∠PQA=90°-∠AQO=90°-(45°+
| 1 |
| 2 |
=45°-
| 1 |
| 2 |
∴P、A、E、Q四点共圆.
(2)连接OE、OF、OC,如图2.
∵P、A、E、Q四点共圆,∠QPE=∠EPA
∴EQ=EA.
在△QEO和△AEO中,
|
∴△QEO≌△AEO(SSS),
∴∠QOE=∠AOE.
∵∠QPE+∠EPA+∠EOP+∠QOE=90°,
∴2∠EPA+2∠EOP=90°,

∴∠EPA+∠EOP=45°,
∴∠FEO=∠EPA+∠EOP=45°.
∵OC=OB,∴∠OCB=∠OBC=45°,
∴∠FEO=∠FCO=45°,
∴C、E、O、F四点共圆,
∴∠EOF+∠ECF=180°,
∴∠EOF=90°.
∵∠AOC=2∠B=90°,
∴∠EOF=∠AOC,
∴∠AOE=∠COF.
在△AEO和△CFO中,
|
∴△AEO≌△CFO(ASA).
∴AE=CF=a,
∴AC=BC=CF+BF=a+b,
∴CE=AC-AE=b.
∵∠ECF=90°,
∴EF=
| CF2+CE2 |
| a2+b2 |
点评:本题主要考查了四点共圆的判定、切线的性质、圆周角定理、圆内接四边形的性质、全等三角形的判定与性质、等腰三角形的性质、勾股定理等知识,综合性比较强,难度比较大.证到∠PQA=45°-
∠QPO=∠PEA是解决第(1)小题的关键,证到C、E、O、F四点共圆及△AEO≌△CFO是解决第(2)小题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
下列模拟掷硬币的实验不正确的是( )
| A、用计算器随机地取数,取奇数相当于下面朝上,取偶数相当于硬币正面朝下 |
| B、袋中装两个小球,分别标上1和2,随机地摸,摸出1表示硬币正面朝上 |
| C、在没有大小王的扑克中随机地抽一张牌,抽到红色牌表示硬币正面朝上 |
| D、将1、2、3、4、5分别写在5张纸上,并搓成团,每次随机地取一张,取到奇数号表示硬币正面朝上 |
已知
是二次根式,则x应满足的条件是( )
|
| A、x>0 | B、x≤0 |
| C、x≥-3 | D、x>-3 |
 如图,四边形ABCD中,∠A=60°,∠B=∠D=90°,AB=4,CD=2,求BC和AD的长.
如图,四边形ABCD中,∠A=60°,∠B=∠D=90°,AB=4,CD=2,求BC和AD的长.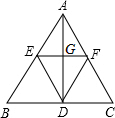 在△ABC中,AB=AC=5,BC=6,AD⊥BC,EF∥BC,则△EDF的最大面积为
在△ABC中,AB=AC=5,BC=6,AD⊥BC,EF∥BC,则△EDF的最大面积为