题目内容
 如图,△ABC中,∠BAC=90°,∠C=30°,AD平分∠BAC交BC于D,AB=
如图,△ABC中,∠BAC=90°,∠C=30°,AD平分∠BAC交BC于D,AB=| 3 |
考点:勾股定理,角平分线的性质,含30度角的直角三角形
专题:
分析:过B作BE∥AC交AD的延长线于E,求出AC、BC的长,求出EB=AB=
+1,证△BDE∽△CDA,得出比例式,代入求出即可.
| 3 |
解答:解:
过B作BE∥AC交AD的延长线于E,
∵△ACB中,∠BAC=90°,AB=
+1,∠C=30°,
∴BC=2AB=2(
+1)=2
+2,
由勾股定理得:AC=
AB=
(
+1)=3+
,
∵BE∥AC,
∴∠E=∠CAD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠E=∠BAD,
∴BE=AB=
+1,
∵BE∥AC,
∴△BDE∽△CDA,
∴
=
,
∴
=
,
解得:CD=2
.

过B作BE∥AC交AD的延长线于E,
∵△ACB中,∠BAC=90°,AB=
| 3 |
∴BC=2AB=2(
| 3 |
| 3 |
由勾股定理得:AC=
| 3 |
| 3 |
| 3 |
| 3 |
∵BE∥AC,
∴∠E=∠CAD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠E=∠BAD,
∴BE=AB=
| 3 |
∵BE∥AC,
∴△BDE∽△CDA,
∴
| BE |
| AC |
| BD |
| DC |
∴
| ||
3+
|
2
| ||
| CD |
解得:CD=2
| 3 |
点评:本题考查了勾股定理,含30度角的直角三角形性质,等腰三角形的判定,相似三角形的性质和判定的应用,解此题的关键是得出关于CD的方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列模拟掷硬币的实验不正确的是( )
| A、用计算器随机地取数,取奇数相当于下面朝上,取偶数相当于硬币正面朝下 |
| B、袋中装两个小球,分别标上1和2,随机地摸,摸出1表示硬币正面朝上 |
| C、在没有大小王的扑克中随机地抽一张牌,抽到红色牌表示硬币正面朝上 |
| D、将1、2、3、4、5分别写在5张纸上,并搓成团,每次随机地取一张,取到奇数号表示硬币正面朝上 |
某商品的进价是400元,标价为600元,折价销售时的利润为5%,问此商品是按几折销售的?设此商品按x%销售,由题意得方程为( )
| A、600•x%=400×5% |
| B、400(1+5%)=6000•x% |
| C、400(1-5%)+600•x% |
| D、600(1-5%)=400•x% |
已知
是二次根式,则x应满足的条件是( )
|
| A、x>0 | B、x≤0 |
| C、x≥-3 | D、x>-3 |
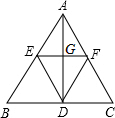 在△ABC中,AB=AC=5,BC=6,AD⊥BC,EF∥BC,则△EDF的最大面积为
在△ABC中,AB=AC=5,BC=6,AD⊥BC,EF∥BC,则△EDF的最大面积为 如图,在⊙O中,弦AB,CD相交于点P,且AB=CD,求证:AC=BD.
如图,在⊙O中,弦AB,CD相交于点P,且AB=CD,求证:AC=BD.