题目内容
8．若关于x的一元二次方程ax2+x-1=0有实数根，则a的取值范围是（ ）| A． | a$≥-\frac{1}{4}$且a≠0 | B． | a$≤-\frac{1}{4}$ | C． | a$≥-\frac{1}{4}$ | D． | a$≤-\frac{1}{4}$且a≠0 |
分析 根据一元二次方程的定义和判别式的意义得到a≠0且△=12-4×a×（-1）≥0，然后求出两不等式的公共部分即可．
解答 解：根据题意得a≠0且△=12-4×a×（-1）≥0，
解得a≥-$\frac{1}{4}$且a≠0．
故选A．
点评 本题考查了根的判别式：一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：当△＞0时，方程有两个不相等的两个实数根；当△=0时，方程有两个相等的两个实数根；当△＜0时，方程无实数根．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
16．
根据图①的面积可以说明多项式的乘法运算（2a+b）（a+b）=2a2+3ab+b2，那么根据图②的面积可以说明多项式的乘法运算是（ ）
根据图①的面积可以说明多项式的乘法运算（2a+b）（a+b）=2a2+3ab+b2，那么根据图②的面积可以说明多项式的乘法运算是（ ）| A． | （a+3b）（a+b）=a2+4ab+3b2 | B． | （a+3b）（a+b）=a2+3b2 | ||
| C． | （b+3a）（b+a）=b2+4ab+3a2 | D． | （a+3b）（a-b）=a2+2ab-3b2 |
问题背景：在△ABC中，AB、BC、AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$，求这个三角形的面积．佳佳同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处）．如图①所示，这样不需求△ABC的高，而借用网格就能计算出它的面积．
13．
已知点P（0，1），Q（5，4），点M在x轴上运动，当MP+MQ的值最小时，点M的坐标为（ ）
已知点P（0，1），Q（5，4），点M在x轴上运动，当MP+MQ的值最小时，点M的坐标为（ ）| A． | （0，0） | B． | （1，0） | C． | （3，0） | D． | （5，0） |
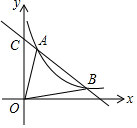如图，一次函数y1=-x+4与反比例函数y2=$\frac{3}{x}$（x＞0）的图象交于A、B两点