题目内容
17.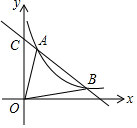 如图,一次函数y1=-x+4与反比例函数y2=$\frac{3}{x}$(x>0)的图象交于A、B两点
如图,一次函数y1=-x+4与反比例函数y2=$\frac{3}{x}$(x>0)的图象交于A、B两点(1)求点A、B 的坐标
(2)直接写出不等式-x+4<$\frac{3}{x}$的解.
分析 (1)通过解方程组$\left\{\begin{array}{l}y=-x+4\\ y=\frac{3}{x}\end{array}\right.$可得到A、B两点的坐标;
(2)观察图象,写出第一象限内反比例函数图象在一次函数图象上方所对应的自变量的范围即可.
解答 解:(1)解方程组$\left\{\begin{array}{l}y=-x+4\\ y=\frac{3}{x}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,
所以A(1,3),B(3,1);
(2)不等式-x+4<$\frac{3}{x}$的解为0<x<1或x>3.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
8.若关于x的一元二次方程ax2+x-1=0有实数根,则a的取值范围是( )
| A. | a$≥-\frac{1}{4}$且a≠0 | B. | a$≤-\frac{1}{4}$ | C. | a$≥-\frac{1}{4}$ | D. | a$≤-\frac{1}{4}$且a≠0 |
12.下列计算正确的是( )
| A. | x2•x2=2x4 | B. | (-2a)3=-8a3 | C. | (a3)-2=a-5 | D. | m3÷m3=m |
9.下列计算正确的是( )
| A. | a3•a5=a15 | B. | a6÷a2=a3 | C. | (-2a3)2=4a6 | D. | a3+a3=2a6 |
7.已知A(x1,y1)、B(x2,y2)两点都在函数y=$\frac{1}{x}$的图象上,且x1<x2<0,则下列结论正确的是( )
| A. | y1<y2<0 | B. | y1>y2>0 | C. | y2>y1>0 | D. | y2<y1<0 |
 一辆轿车离开某城市的距离y(km)与行驶时间t(h)之间的关系式为y=kt+30,图象如图所示,在1h到3h之间,轿车行驶的路程是120km.
一辆轿车离开某城市的距离y(km)与行驶时间t(h)之间的关系式为y=kt+30,图象如图所示,在1h到3h之间,轿车行驶的路程是120km.