题目内容
已知,点A、B、C、D四点在一条直线上,AB=6cm,DB=1cm,点C是线段AD的中点,请画出相应的示意图,并求出此时线段BC的长度.
考点:两点间的距离
专题:
分析:分类讨论:点D在线段AB上,点D在线段AB的延长线上,根据线段的和差,可得AD的长,根据线段中点的性质,可得AC的长,再根据线段的和差,可得答案.
解答:解:当点D在线段AB上时,如图:
 ,
,
由线段的和差,得
AD=AB-BD=6-1=5cm,
由C是线段AD的中点,得
AC=
AD=
×5=
cm,
由线段的和差,得
BC=AB-AC=6-
=
cm;
当点D在线段AB的延长线上时,如图:
 ,
,
由线段的和差,得
AD=AB+BD=6+1=7cm,
由C是线段AD的中点,得
AC=
AD=
×7=
cm,
由线段的和差,得
BC=AB-AC=6-
=
cm.
 ,
,由线段的和差,得
AD=AB-BD=6-1=5cm,
由C是线段AD的中点,得
AC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
由线段的和差,得
BC=AB-AC=6-
| 5 |
| 2 |
| 7 |
| 2 |
当点D在线段AB的延长线上时,如图:
 ,
,由线段的和差,得
AD=AB+BD=6+1=7cm,
由C是线段AD的中点,得
AC=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
由线段的和差,得
BC=AB-AC=6-
| 7 |
| 2 |
| 5 |
| 2 |
点评:本题考查了两点间的距离,利用了线段的和差,线段中点的性质,分类讨论是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
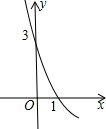 如图表示的是二次函数y=ax2+bx+c的图象的一部分,已知图象经过点(0,3)与(1,0),若s=a-b,则下列描述s的取值范围最合适的一个选项是( )
如图表示的是二次函数y=ax2+bx+c的图象的一部分,已知图象经过点(0,3)与(1,0),若s=a-b,则下列描述s的取值范围最合适的一个选项是( )| A、-3<s<3 | B、s>0 |
| C、s>3 | D、0<s<3 |
 如图,防洪大堤的横断面是梯形,坝高AH=6米,背水坡AB的坡度i=3:4,则斜坡AB的长为
如图,防洪大堤的横断面是梯形,坝高AH=6米,背水坡AB的坡度i=3:4,则斜坡AB的长为 如图,点P,C在线段AB上,AC=6cm,PB=10cm,若P是AC的中点,则CB的长是
如图,点P,C在线段AB上,AC=6cm,PB=10cm,若P是AC的中点,则CB的长是 如图所示,在等腰△ABC中,BC=AC,∠ACB=90°,D、E为斜边AB上的点,且∠DCE=45°
如图所示,在等腰△ABC中,BC=AC,∠ACB=90°,D、E为斜边AB上的点,且∠DCE=45° 尺规作图:如图,在Rt△ABC中,∠C=90°.
尺规作图:如图,在Rt△ABC中,∠C=90°.