题目内容
 如图所示,在等腰△ABC中,BC=AC,∠ACB=90°,D、E为斜边AB上的点,且∠DCE=45°
如图所示,在等腰△ABC中,BC=AC,∠ACB=90°,D、E为斜边AB上的点,且∠DCE=45°求证:DE2=AD2+BE2.
考点:旋转的性质,全等三角形的判定与性质,勾股定理
专题:证明题
分析:如图,将△ADC绕点C逆时针旋转90°到△CBF的位置;证明∠A=∠ABC=∠CBF=45°,得到EF2=AD2+BE2
证明△DCE≌△FCE,得到DE=EF,故DE2=AD2+BE2.
证明△DCE≌△FCE,得到DE=EF,故DE2=AD2+BE2.
解答: 证明:如图,将△ADC绕点C逆时针旋转90°到△CBF的位置;
证明:如图,将△ADC绕点C逆时针旋转90°到△CBF的位置;
则CD=CE,AD=BF;∠BCF=∠ACD,∠CBF=∠A;
∵BC=AC,∠ACB=90°,
∴∠A=∠ABC=∠CBF=45°,
∴∠EBF=90°,EF2=BE2+BF2=AD2+BE2;
∵∠DCE=45°,∠ACB=90°,
∴∠ACD+∠BCE=90°-45°=45°,而∠ACD=∠BCF,
∴∠ECF=∠ECD=45°;在△DCE与△FCE中,
,
∴△DCE≌△FCE(SAS),
∴DE=EF,
∴DE2=AD2+BE2.
 证明:如图,将△ADC绕点C逆时针旋转90°到△CBF的位置;
证明:如图,将△ADC绕点C逆时针旋转90°到△CBF的位置;则CD=CE,AD=BF;∠BCF=∠ACD,∠CBF=∠A;
∵BC=AC,∠ACB=90°,
∴∠A=∠ABC=∠CBF=45°,
∴∠EBF=90°,EF2=BE2+BF2=AD2+BE2;
∵∠DCE=45°,∠ACB=90°,
∴∠ACD+∠BCE=90°-45°=45°,而∠ACD=∠BCF,
∴∠ECF=∠ECD=45°;在△DCE与△FCE中,
|
∴△DCE≌△FCE(SAS),
∴DE=EF,
∴DE2=AD2+BE2.
点评:该题主要考查了旋转变换的性质、全等三角形的判定及其性质、勾股定理等几何知识点及其应用问题;解题的关键是作旋转变换,将分散的条件集中到某个三角形中.

练习册系列答案
相关题目
 如图,C是线段AB上的一点,M是线段AC的中点,若AB=8cm,MC=3cm,则BC的长是( )
如图,C是线段AB上的一点,M是线段AC的中点,若AB=8cm,MC=3cm,则BC的长是( )| A、2cm | B、3cm |
| C、4cm | D、6cm |
 如图,将一副三角板按如图所示方式摆放,点A,B,D在同一条直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,DE=8,试求BD的长.
如图,将一副三角板按如图所示方式摆放,点A,B,D在同一条直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,DE=8,试求BD的长.
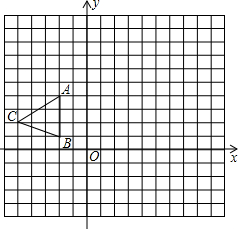 如图在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
如图在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2). 已知,如图,线段AD=10cm,点B,C都是线段AD上的点,且AC=7cm,BD=4cm,若E,F分别是线段AB,CD的中点,求BC与EF的长度.
已知,如图,线段AD=10cm,点B,C都是线段AD上的点,且AC=7cm,BD=4cm,若E,F分别是线段AB,CD的中点,求BC与EF的长度. 如图,某校准备在校内一块四边形ABCD草坪内栽上一颗银杏树,要求银杏树的位置点P到边AB,BC的距离相等,并且点P到点A,D的距离也相等,请用尺规作图作出银杏树的位置点P(不写作法,保留作图痕迹)
如图,某校准备在校内一块四边形ABCD草坪内栽上一颗银杏树,要求银杏树的位置点P到边AB,BC的距离相等,并且点P到点A,D的距离也相等,请用尺规作图作出银杏树的位置点P(不写作法,保留作图痕迹)