Question

在一条笔直的公路MN的同一旁有两个新开发区A、B，已知AB=20km，直线AB与公路MN的夹角∠AON=30°，新开发区B到公路MN的距离BC=5km．现要在MN上某点P处向新开发区A、B修两条公路PA、PB，使点P到新开发区A、B的距离之和最短，此时PA+PB等于（　　）

• A、10km
• B、20km
• C、22km
• D、10

  7

  km

Answer 1

考点：轴对称-最短路线问题

专题：

分析：作B关于NC的对称点B′，连接AB′，作AD⊥BC于点D．则B′C=BC=5km．AD∥NO，∠DAB=∠BOC=30°．解直角三角形求得DB=AB•sin∠DAB=20×

1

2

=10（km）．AD=AB•cos∠DAB=20×

3

2

=10

3

（km）．从而求得DB′=10+5+5=20（km）．根据勾股定理即可求得PA+PB的最短距离．

解答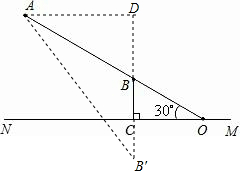：解：作B关于NC的对称点B′，连接AB′，作AD⊥BC于点D．则B′C=BC=5km．AD∥NO，∠DAB=∠BOC=30°．
∵在直角△ABD中，sin∠DAB=

DB

AB

，cos∠DAB=

AD

AB

，
∴DB=AB•sin∠DAB=20×

1

2

=10（km）．AD=AB•cos∠DAB=20×

3

2

=10

3

（km）．
则在直角△AB′D中，AB′=

AD2+DB′

=

(10 3 )2+202

=10

7

，
故选D．

点评：此题主要考查轴对称-最短路线问题，利用轴对称的性质来综合解三角形是本题的关键．