题目内容
已知:a、b为实数,且a2+ab+b2=5,a2-ab+b2=k,求k的最大值和最小值,并求出当k取到最大值和最小值时,对应的a、b的值分别是多少?
考点:配方法的应用
专题:
分析:由两个等式可求出a+b、ab的表达式,然后结合一元二次方程根与系数的关系得到a,b是关于方程x2±
+
=0的两个实根,由二次根式有意义的条件得到k的最大值;由一元二次方程的根的判别式得到k的最小值.
|
| 5-k |
| 2 |
解答:解:∵a2+ab+b2=5,①
a2-ab+b2=k,②
∴由①-②得 ab=
,③
把③代入①,解得a+b=±
(k≤15),④
∴a,b是关于方程x2±
+
=0的两个实根,
由△=
-4×
≥0,
解得 k≥
.
故k的取值范围为:
≤k≤15.则k的最大值是15、最小值是
.
①当k=15时,
,
解得
或
.
②当k=
时,
,解得
.
a2-ab+b2=k,②
∴由①-②得 ab=
| 5-k |
| 2 |
把③代入①,解得a+b=±
|
∴a,b是关于方程x2±
|
| 5-k |
| 2 |
由△=
| 15-k |
| 2 |
| 5-k |
| 2 |
解得 k≥
| 5 |
| 3 |
故k的取值范围为:
| 5 |
| 3 |
| 5 |
| 3 |
①当k=15时,
|
解得
|
|
②当k=
| 5 |
| 3 |
|
|
点评:本题考查了配方法的应用,解题时,利用了完全平方公式和完全平方公式的变形求得ab、a+b的值是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

 如图,AB,CD相交于点O,AB=CD,
如图,AB,CD相交于点O,AB=CD, 在一条笔直的公路MN的同一旁有两个新开发区A、B,已知AB=20km,直线AB与公路MN的夹角∠AON=30°,新开发区B到公路MN的距离BC=5km.现要在MN上某点P处向新开发区A、B修两条公路PA、PB,使点P到新开发区A、B的距离之和最短,此时PA+PB等于( )
在一条笔直的公路MN的同一旁有两个新开发区A、B,已知AB=20km,直线AB与公路MN的夹角∠AON=30°,新开发区B到公路MN的距离BC=5km.现要在MN上某点P处向新开发区A、B修两条公路PA、PB,使点P到新开发区A、B的距离之和最短,此时PA+PB等于( )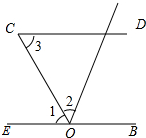 已知,∠1=∠2,∠2=∠3.求证:CD∥EB.
已知,∠1=∠2,∠2=∠3.求证:CD∥EB.