题目内容
 如图所示,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A,C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A,B和D(4,-
如图所示,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A,C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A,B和D(4,-| 2 |
| 3 |
考点:待定系数法求二次函数解析式
专题:
分析:首先根据题意确定A、B、C、D点的坐标值,因为抛物线y=ax2+bx+c经过点A,B和点 D(4,-
),将A、B、D点的坐标值代入抛物线联立解得a、b、c的值.
| 2 |
| 3 |
解答:解:由题意得A(0,-2)、B(2,-2)、C(2,0),
∵抛物线y=ax2+bx+c经过点A,B和点 D(4,-
),
∴
,
解得
,
∴抛物线的解析式为y=
x2-
x-2.
∵抛物线y=ax2+bx+c经过点A,B和点 D(4,-
| 2 |
| 3 |
∴
|
解得
|
∴抛物线的解析式为y=
| 1 |
| 6 |
| 1 |
| 3 |
点评:本题主要考查了待定系数法求二次函数解析式、函数图象交点的求法,熟练掌握待定系数法是解题的关键.

练习册系列答案
相关题目
 在一条笔直的公路MN的同一旁有两个新开发区A、B,已知AB=20km,直线AB与公路MN的夹角∠AON=30°,新开发区B到公路MN的距离BC=5km.现要在MN上某点P处向新开发区A、B修两条公路PA、PB,使点P到新开发区A、B的距离之和最短,此时PA+PB等于( )
在一条笔直的公路MN的同一旁有两个新开发区A、B,已知AB=20km,直线AB与公路MN的夹角∠AON=30°,新开发区B到公路MN的距离BC=5km.现要在MN上某点P处向新开发区A、B修两条公路PA、PB,使点P到新开发区A、B的距离之和最短,此时PA+PB等于( )| A、10km | ||
| B、20km | ||
| C、22km | ||
D、10
|
下列四个腾讯软件图标中,属于轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
下列图形中,既是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
当m≤3时,下列等式一定成立的是( )
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
 如图,AB∥CD,∠1=∠A,求证:EF∥CD.
如图,AB∥CD,∠1=∠A,求证:EF∥CD.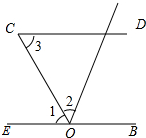 已知,∠1=∠2,∠2=∠3.求证:CD∥EB.
已知,∠1=∠2,∠2=∠3.求证:CD∥EB. 如图,程程和小磊在他们家附近的公园中玩跷跷板,跷跷板上的横板AD通过点B,且可以绕点B上下转动,木桩BC与路面AC始终成90°,当处在如图所示的位置时∠ABC=60°,则这个跷跷板上下最多可以转动( )
如图,程程和小磊在他们家附近的公园中玩跷跷板,跷跷板上的横板AD通过点B,且可以绕点B上下转动,木桩BC与路面AC始终成90°,当处在如图所示的位置时∠ABC=60°,则这个跷跷板上下最多可以转动( )