题目内容
7. 已知关于x的一元二次方程x2+2x+$\frac{k-1}{2}$=0
已知关于x的一元二次方程x2+2x+$\frac{k-1}{2}$=0(1)若此方程有两个不相等的实数根,求k的取值范围;
(2)当此方程有一根为零时,将二次函数y=x2+2x+$\frac{k-1}{2}$图象x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分保持不变,翻折后图象与原图象x轴上方的部分组成给一个“W”形状的新图象,观察新图象发现:
①当直线y=m与该新图象有4个公共点时,实数m的取值范围是0<m<1.
②当直线y=$\frac{1}{2}$x+b与该新图象恰好有3个公共点时,直接写出实数b的值.
分析 (1)根据一元二次方程根的判别式即可得出;
(2)先根据原抛物线的解析式得出翻折后得出新图象的解析式,进而画出图象,①根据图象直接判断出来;②结合图形确定出直线的位置即可求出b的值.
解答 解:(1)关于x的一元二次方程x2+2x+$\frac{k-1}{2}$=0有两个不相等的实数根,
∴△=22-4×$\frac{k-1}{2}$>0,
∴k<3;
(2)∵关于x的一元二次方程x2+2x+$\frac{k-1}{2}$=0方程有一根为零
∴当x=0时,k=1,二次函数解析式为y=x2+2x=(x+1)2-1,
∴抛物线y=x2+2x的顶点坐标为(-1,-1),
当y=0时,x2+2x=0,解得x1=0,x2=-2,
则抛物线y=x2+2x与x轴的交点为(-2,0),(0,0),
把抛物线y=x2+2x图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=-(x+1)2+1(-2≤x≤0),顶点坐标M(-1,1),
如图,
①当直线y=m与该新图象有4个公共点时,0<m<1
故答案为0<m<1;
②把直线y=$\frac{1}{2}$x向上平移,当平移后的直线y=$\frac{1}{2}$x+b过点A时,直线y=$\frac{1}{2}$x+b与该新图象恰好有三个公共点,
∴$\frac{1}{2}$×(-2)+b=0,解得b=1;
当直线y=$\frac{1}{2}$x+b与抛物线y=-(x+1)2+1(-2≤x≤0)相切时,直线y=$\frac{1}{2}$x+b与该新图象恰好有三个公共点,
即-(x+1)2+1=$\frac{1}{2}$x+b有相等的实数解,整理得x2+$\frac{5}{2}$x+b=0,△=($\frac{5}{2}$)2-4b=0,解得b=$\frac{25}{16}$,
所以b的值为1或$\frac{25}{16}$.
点评 此题主要考查了翻折的性质,一元二次方程根的判别式,抛物线的性质,确定翻折后抛物线的关系式;利用数形结合的方法是解本题的关键,画出函数图象是解本题的难点.

 如图,ABCD是⊙O内接矩形,半径r=2,AB=2,E,F分别是AC,CD上的动点,且AE=CF,则BE+BF的最小值是( )
如图,ABCD是⊙O内接矩形,半径r=2,AB=2,E,F分别是AC,CD上的动点,且AE=CF,则BE+BF的最小值是( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{7}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
| A. | 一个有理数的绝对值一定比0大 | |
| B. | 两个数比较大小,绝对值大的反而小 | |
| C. | 相反数等于它本身的数是0 | |
| D. | 若a>0,b<0且|a|>|b|,则a+b<0 |
| A. | 8m3n+4mn2=2mn(4m2+2n) | B. | m3-n3=(m-n)(m2+mn+n2) | ||
| C. | (y+1)(y-3)=-(3-y)(y+1) | D. | 4yz-2y2z+z=2y(2z-yz)+z |
| A. | (-$\frac{2}{3}$)-2=$\frac{4}{9}$ | B. | $\frac{-a+b}{c}$=-$\frac{a+b}{c}$ | ||
| C. | ($\frac{2{a}^{2}}{3b}$)3=$\frac{8{a}^{5}}{9{b}^{3}}$ | D. | $\frac{-a-b}{-a+b}$=$\frac{a+b}{a-b}$ |
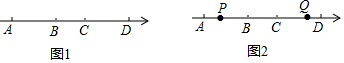 点A、B、C、D在数轴上的位置如图1所示,已知AB=3,BC=2,CD=4.
点A、B、C、D在数轴上的位置如图1所示,已知AB=3,BC=2,CD=4.