题目内容
17.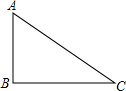 △ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )
△ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )| A. | $2\sqrt{5}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 4 |
分析 根据正切定义得到tan∠C=$\frac{AB}{BC}$=$\frac{1}{2}$,则可设AB=x,BC=2x,利用勾股定理计算出AC=$\sqrt{5}$x,所以$\sqrt{5}$x=$\sqrt{5}$,解得x=1,然后计算2x即可得到BC的长.
解答 解:∵∠B=90°,
∴tan∠C=$\frac{AB}{BC}$=$\frac{1}{2}$,
设AB=x,则BC=2x,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{5}$x,
∴$\sqrt{5}$x=$\sqrt{5}$,解得x=1,
∴BC=2x=2.
故选B.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
相关题目
12.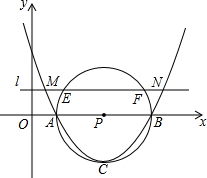 如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
 如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )| A. | 2$\sqrt{6}$ | B. | 4$\sqrt{2}$ | C. | 5 | D. | 6 |
2. 如图,有一个工件,它的左视图是( )
如图,有一个工件,它的左视图是( )
 如图,有一个工件,它的左视图是( )
如图,有一个工件,它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
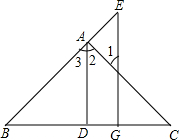 如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,可得AD平分∠BAC,理由如下:
如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,可得AD平分∠BAC,理由如下: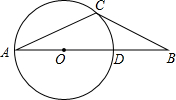 如图,在△ABC中,2∠A+∠B=90°,点0在AB边上,以O点为圆心的圆经过A、C 两点,交AB于D点.
如图,在△ABC中,2∠A+∠B=90°,点0在AB边上,以O点为圆心的圆经过A、C 两点,交AB于D点.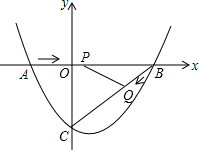 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C,tan∠BAC=2.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C,tan∠BAC=2.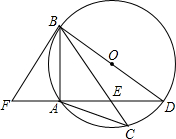 如图,在⊙O中,AB=AC,BD为直径,弦AD与BC相交于点E,延长DA到F,使∠ABF=∠ABC.
如图,在⊙O中,AB=AC,BD为直径,弦AD与BC相交于点E,延长DA到F,使∠ABF=∠ABC.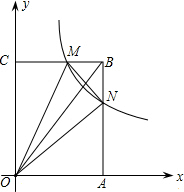 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$在第一象限的部分经过矩形OABC的中心E,分别与矩形的BC、BA边相交于M、N,△BMN的面积等于9,则k的值为8.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$在第一象限的部分经过矩形OABC的中心E,分别与矩形的BC、BA边相交于M、N,△BMN的面积等于9,则k的值为8. 如图是由五块积木搭成的,这几块积木都是相同的正方体,请你画出从这个图形的正面看、上面看、左面看的平面图.
如图是由五块积木搭成的,这几块积木都是相同的正方体,请你画出从这个图形的正面看、上面看、左面看的平面图.