题目内容
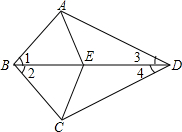 已知:如图,∠1=∠2,∠3=∠4,点E在BD上,连结AE、CE,求证:AE=CE.
已知:如图,∠1=∠2,∠3=∠4,点E在BD上,连结AE、CE,求证:AE=CE.考点:全等三角形的判定与性质
专题:证明题
分析:先由条件可以得出△ABD≌△CBD就可以得出AD=CD,再证明△AED≌△CED就可以得出结论.
解答:证明:在△ABD和△CBD中,
,
∴△ABD≌△CBD(ASA),
∴AD=CD.
在△AED和△CED中,
,
∴△AED≌△CED(SAS),
∴AE=CE.
|
∴△ABD≌△CBD(ASA),
∴AD=CD.
在△AED和△CED中,
|
∴△AED≌△CED(SAS),
∴AE=CE.
点评:本题考查了运用ASA和SAS证明三角形全等的运用,全等三角形的性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 已知:如图,AB∥CD,AB=CD.求证:AD∥BC.
已知:如图,AB∥CD,AB=CD.求证:AD∥BC.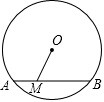 如图,⊙O的半径为5,M是
如图,⊙O的半径为5,M是
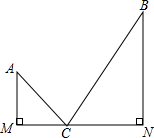 如图:知:AM⊥MN,BN⊥MN,垂足分别为M,N,点C是MN上使AC+BC的值最小的点.若AM=3,BN=5,MN=15,则AC+BC=
如图:知:AM⊥MN,BN⊥MN,垂足分别为M,N,点C是MN上使AC+BC的值最小的点.若AM=3,BN=5,MN=15,则AC+BC=