题目内容
10.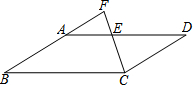 如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{8}$ED,则$\frac{FA}{AB}$的值为( )
如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{8}$ED,则$\frac{FA}{AB}$的值为( )| A. | $\frac{15}{13}$ | B. | $\frac{8}{5}$ | C. | $\frac{5}{8}$ | D. | $\frac{15}{8}$ |
分析 设AE=5x,DE=8x,AD=13x,根据平行四边形的性质得出BC=AD=13x,BC∥AD,根据相似三角形的判定得出△FAE∽△FBC,根据相似三角形的性质求出$\frac{FA}{FB}$=$\frac{AE}{BC}$=$\frac{5}{13}$,即可求出答案.
解答 解:∵AE=$\frac{5}{8}$ED,
∴设AE=5x,DE=8x,AD=13x,
∵四边形ABCD是平行四边形,
∴BC=AD=13x,BC∥AD,
∴△FAE∽△FBC,
∴$\frac{FA}{FB}$=$\frac{AE}{BC}$=$\frac{5x}{13x}$=$\frac{5}{13}$,
∴$\frac{FA}{AB}$=$\frac{5}{13-5}$=$\frac{5}{8}$,
故选C.
点评 本题考查了平行四边形的性质,相似三角形的性质和判定等知识点,能求出△FAE∽△FBC是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15. 如图,这个棱柱的左视图是( )
如图,这个棱柱的左视图是( )
 如图,这个棱柱的左视图是( )
如图,这个棱柱的左视图是( )| A. |  | B. |  | C. |  | D. |  |
2. 如图,在⊙O中,弦AB与CD交于点M,∠C=45°,∠AMD=75°,则∠D的度数是( )
如图,在⊙O中,弦AB与CD交于点M,∠C=45°,∠AMD=75°,则∠D的度数是( )
 如图,在⊙O中,弦AB与CD交于点M,∠C=45°,∠AMD=75°,则∠D的度数是( )
如图,在⊙O中,弦AB与CD交于点M,∠C=45°,∠AMD=75°,则∠D的度数是( )| A. | 15° | B. | 25° | C. | 30° | D. | 75° |
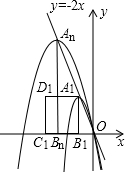 我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线: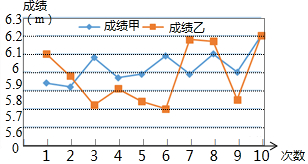 如图是甲、乙两名跳远运动员的10次测验成绩(单位:米)的折线统计图,观察图形,写出甲、乙这10次跳远成绩之间的大小关系:S甲2<S乙2(填“>“或“<”)
如图是甲、乙两名跳远运动员的10次测验成绩(单位:米)的折线统计图,观察图形,写出甲、乙这10次跳远成绩之间的大小关系:S甲2<S乙2(填“>“或“<”)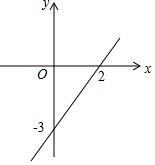 已知一次函数的图象如图所示.
已知一次函数的图象如图所示.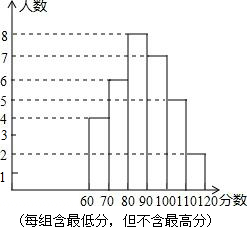 某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频数直方图,如图所示.
某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频数直方图,如图所示.