题目内容
5.若直线2y+x=a与直线4y+3x=15的交点在第一象限,且a是整数,求a的值.分析 利用两直线相交问题,通过解方程组$\left\{\begin{array}{l}{2y+x=a}\\{4y+3x=15}\end{array}\right.$得两直线的交点坐标为(15-2a,$\frac{3a-15}{2}$),再利用第一象限点的坐标特征得到15-2a>0且$\frac{3a-15}{2}$>0,然后解不等式组后找出整数a即可.
解答 解:解方程组$\left\{\begin{array}{l}{2y+x=a}\\{4y+3x=15}\end{array}\right.$得$\left\{\begin{array}{l}{x=15-2a}\\{y=\frac{1}{2}(3a-15)}\end{array}\right.$,
所以两直线的交点坐标为(15-2a,$\frac{3a-15}{2}$),
因为交点在第一象限,
所以15-2a>0且$\frac{3a-15}{2}$>0,解得5<a<7.5,
所以整数a为6或7.
点评 本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
18.下列各式计算正确的是( )
| A. | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{3}$ |
10.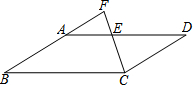 如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{8}$ED,则$\frac{FA}{AB}$的值为( )
如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{8}$ED,则$\frac{FA}{AB}$的值为( )
 如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{8}$ED,则$\frac{FA}{AB}$的值为( )
如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{8}$ED,则$\frac{FA}{AB}$的值为( )| A. | $\frac{15}{13}$ | B. | $\frac{8}{5}$ | C. | $\frac{5}{8}$ | D. | $\frac{15}{8}$ |
17.已知点A(-1,0),B(2,0),在y轴上存在一点C,使三角形ABC的面积为6,则点C的坐标为( )
| A. | (0,4) | B. | (0,2) | C. | (0,2)或(0,-2) | D. | (0,4)或(0,-4) |
15.近年来空气净化器成为很多家庭的新电器.某品牌的空气净化器厂家为进一步了解市场,制定生产计划,根据2016年下半年销售情况绘制了统计表,其中同比增长率=($\frac{当月销售量}{去年同月销售量}$-1)×100%,下面有四个推断:
①2016年下半年各月销售量均比2015年同月销售量增多;
②2016年下半年销售量增长幅度最大的是11月至12月;
③2015年9月的销售量约为9.3万台;
④若保持相同的增长率,则2017年10月的销售量可约为15.4万台;
其中正确的是( )
①2016年下半年各月销售量均比2015年同月销售量增多;
②2016年下半年销售量增长幅度最大的是11月至12月;
③2015年9月的销售量约为9.3万台;
④若保持相同的增长率,则2017年10月的销售量可约为15.4万台;
其中正确的是( )
| 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
| 销售量 | 8 | 9.3 | 9.8 | 13.4 | 19.7 | 36 |
| 同比增长率 | -2.3% | 6.5% | 5.2% | 15.1% | 20.7% | 35.9% |
| A. | ①③④ | B. | ②③④ | C. | ②③ | D. | ②④ |
 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为3$\sqrt{3}$.
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为3$\sqrt{3}$.