题目内容
17. 如图,已知四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于 G.
如图,已知四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于 G.(1)求证:$\frac{CF}{AD}$=$\frac{AB}{AE}$;
(2)求证:$\frac{EF}{DE}$+$\frac{FG}{DG}$=1;
(3)若BF=CF,则$\frac{CG}{CA}$=$\frac{1}{2}$;
(4)若$\frac{BF}{CF}$=$\frac{1}{2}$,则$\frac{CG}{CA}$=$\frac{2}{3}$;
(5)设$\frac{BF}{CF}$=x,$\frac{CG}{CA}$=y,求y与x之间的函数关系式.
分析 (1)根据平行四边形的性质得AD∥AB,AD∥BC,AB=CD,再利用平行线分线段成比例定理由CF∥AD得到$\frac{CF}{AD}$=$\frac{CG}{AG}$,由DC∥AE得到$\frac{DC}{AE}$=$\frac{CG}{AG}$,然后利用等量代换即可得到结论;
(2)利用平行线分线段成比例定理,由BF∥AD得到$\frac{EF}{DE}$=$\frac{BF}{AD}$,由CF∥AD得到$\frac{CF}{AD}$=$\frac{FG}{DG}$,则$\frac{EF}{DE}$+$\frac{FG}{DG}$=$\frac{BF}{AD}$+$\frac{CF}{AD}$,然后利用平行四边形的性质即可得到结论;
(3)利用平行线分线段成比例定理,由CD∥BE得到$\frac{DC}{BE}$=$\frac{CF}{BF}$=1,则AE=2DC,然后利用DC∥AE即可得到$\frac{CG}{AG}$=$\frac{DC}{AE}$=$\frac{1}{2}$;
(4)利用平行线分线段成比例定理,由CD∥BE得到$\frac{DC}{BE}$=$\frac{CF}{BF}$=2,则AE=$\frac{3}{2}$DC,然后由DC∥AE得到$\frac{CG}{AG}$=$\frac{DC}{AE}$=$\frac{2}{3}$;
(5)利用平行线分线段成比例定理,由CD∥BE得到$\frac{DC}{BE}$=$\frac{CF}{BF}$=$\frac{1}{x}$,则AE=(1+x)DC,然后由DC∥AE得到$\frac{CG}{AG}$=$\frac{DC}{AE}$=$\frac{1}{1+x}$,于是得到y=$\frac{1}{1+x}$.
解答 解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥AB,AD∥BC,AB=CD,AD=BC,
∵CF∥AD,
∴$\frac{CF}{AD}$=$\frac{CG}{AG}$,
∵DC∥AE,
∴$\frac{DC}{AE}$=$\frac{CG}{AG}$,
∴$\frac{CF}{AD}$=$\frac{CD}{AE}$,
而AB=CD,
∴$\frac{CF}{AD}$=$\frac{AB}{AE}$;
(2)证明:∵BF∥AD,
∴$\frac{EF}{DE}$=$\frac{BF}{AD}$,
∵CF∥AD,
∴$\frac{CF}{AD}$=$\frac{FG}{DG}$,
∴$\frac{EF}{DE}$+$\frac{FG}{DG}$=$\frac{BF}{AD}$+$\frac{CF}{AD}$=$\frac{BF+CF}{AD}$=$\frac{BC}{AD}$=1;
(3)解:∵CD∥BE,
∴$\frac{DC}{BE}$=$\frac{CF}{BF}$,
而BF=CF,
∴DC=BE,
而DC=AB,
∴AE=2DC,
∵DC∥AE,
∴$\frac{CG}{AG}$=$\frac{DC}{AE}$=$\frac{1}{2}$;
(4)解:∵CD∥BE,
∴$\frac{DC}{BE}$=$\frac{CF}{BF}$,
而$\frac{BF}{CF}$=$\frac{1}{2}$,
∴DC=2BE,
而DC=AB,
∴AE=$\frac{3}{2}$DC,
∵DC∥AE,
∴$\frac{CG}{AG}$=$\frac{DC}{AE}$=$\frac{2}{3}$;
故答案为$\frac{1}{2}$,$\frac{2}{3}$;
(5)解:∵CD∥BE,
∴$\frac{DC}{BE}$=$\frac{CF}{BF}$=$\frac{1}{x}$,
∴DC=xBE,
而DC=AB,
∴AE=(1+x)DC,
∵DC∥AE,
∴$\frac{CG}{AG}$=$\frac{DC}{AE}$=$\frac{1}{1+x}$;
即y=$\frac{1}{1+x}$.
点评 本题考查了相似形综合题:熟练掌握平行四边形的性质和平行线分线段成比例定理;本题图中相似三角形较多,要针对每小题选择合适的相似三角形.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案| A. | 与x轴平行 | B. | 与y轴平行 | ||
| C. | 与x轴相交,但不垂直 | D. | 与y轴相交,但不垂直 |
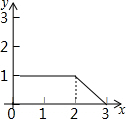
 如图,在矩形ABCD中,AB=2,BC=1,动点P从点A出发,沿路线A→B→C做匀速运动,那么△CDP的面积S与点P运动的路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1,动点P从点A出发,沿路线A→B→C做匀速运动,那么△CDP的面积S与点P运动的路程x之间的函数图象大致是( )