Question

6．在△ABC中，AB，BC，AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$，求这个三角形的面积小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（△ABC的三个顶点都在正方形的顶点处），如图所示，这样不需要求△ABC的高，而借用网格就能计算出它的面积．
（1）请你将△ABC的面积直接填写在横线上．$\frac{7}{2}$
（2）画△DEF，DE、EF、DF三边的长分别为 $\sqrt{2}$、$\sqrt{8}$、$\sqrt{10}$，
①判断三角形的形状，说明理由．
②求这个三角形的面积．

Answer 1

分析 （1）直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案；
（2）①利用勾股定理以及结合勾股定理的逆定理得出答案；
②直接利用直角三角形面积求法得出答案．

解答 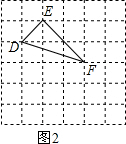解：（1）S_△ABC=3×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×3=$\frac{7}{2}$；
故答案为：$\frac{7}{2}$；

（2）如图2所示：△DEF，即为所求；
①∵（$\sqrt{2}$）²+（$\sqrt{8}$）²=（$\sqrt{10}$）²，
∴△DEF是直角三角形；
②S_△DEF=$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{8}$=2．

点评 此题主要考查了应用设计与作图以及勾股定理、勾股定理逆定理等知识，正确求出三角形面积是解题关键．