题目内容
7. 如图,在矩形ABCD中,AB=2,BC=1,动点P从点A出发,沿路线A→B→C做匀速运动,那么△CDP的面积S与点P运动的路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1,动点P从点A出发,沿路线A→B→C做匀速运动,那么△CDP的面积S与点P运动的路程x之间的函数图象大致是( )| A. | 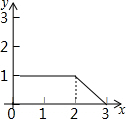 | B. |  | C. |  | D. |  |
分析 运用动点函数进行分段分析,当P在AB上与BC上时,分别求出函数解析式,再结合图象得出符合要求的解析式.
解答 解:CD=AB=2,BC=1,
动点P从点A出发,P点在AB上时,△ABP的高是1,底边是2,所以面积是1,即S=1;
s=1时,是一个常数函数,是一条平行于x轴的直线.
动点P从点B出发,P点在BC上时,BP=x-2,CD=AB=2,
△CDP的面积S=$\frac{1}{2}$×CD×CP=$\frac{1}{2}$×2(2+1-x)=3-x;
S=3-x是一次函数,且y随x的增大而减少,
所以只有A符合要求.
故选A.
点评 此题主要考查了动点函数的应用,注意将函数分段分析得出解析式是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列说法正确的是( )
| A. | 每个命题都有逆命题 | |
| B. | 每个定理都有逆定理 | |
| C. | 原命题与逆命题同为真命题或同为逆命题 | |
| D. | 公理的逆命题是真命题 |
18.下列各数中互为倒数的是( )
| A. | $-\frac{1}{2}$与0.2 | B. | -2与$-\frac{1}{2}$ | C. | $\frac{1}{3}$与-0.33 | D. | -2与|-2| |
15.一元二次方程x2-4x=5的二次项系数、一次项系数、常数项分别为( )
| A. | 1,4,5 | B. | 1,-4,5 | C. | 1,-4,-5 | D. | 1,4,-5 |
12.下列四组条件中,能识别△ABC与△DEF相似的是( )
| A. | ∠A=45°,∠B=55°;∠D=45°∠F=75° | |
| B. | AB=5,BC=4,∠A=45°;DE=10,EF=8,∠D=45° | |
| C. | AB=6,BC=5,∠B=40°;DE=5,EF=6,∠E=40° | |
| D. | BC=4,AC=6,AB=9;DE=6,EF=12,DF=18 |
19.不等式2x-6≤0的非负整数解的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,已知四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于 G.
如图,已知四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于 G.