题目内容
16.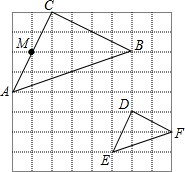 如图,在8×8的正方形网格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上,AC与网格上的直线相交于点M.
如图,在8×8的正方形网格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上,AC与网格上的直线相交于点M.(1)∠ABC的大小;
(2)画出△ABC关于直线AB的对称图形△A1B1C1;
(3)分别求出图中△ABC和△DEF的面积,并写出这两个三角形的边长比与面积比的关系式.
分析 (1)先利用网格特点,根据勾股定理求出△ABC各边的长,然后利用勾股定理说明此三角形为直角三角形,再证明它为等腰直角三角形,从而得到∠ABC的度数;
(2)利用网格特征作出点C关于AB的对称点C1即可得到△A1B1C1;
(3)同样利用勾股定理的逆定理可证明△DEF为直角三角形,∠EDF=90°,再利用三角形面积公式可计算出△ABC和△DEF的面积,从计算结果可得这两个三角形的面积的比等于对应边长比的平方.
解答  解:(1)AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,AB=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
解:(1)AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,AB=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
∵AC2+BC2=AB2,
∴△ABC为直角三角形,∠ACB=90°,
而AC=BC,
∴△ABC为等腰直角三角形,
∴∠ABC=45°;
(2)如图,△A1B1C1为所作;
(3)DE=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,DF=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,EF=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∵DE2+EF2=EF2,
∴△DEF为直角三角形,∠EDF=90°,
∴S△DEF=$\frac{1}{2}$×$\sqrt{5}$×$\sqrt{5}$=$\frac{5}{2}$,
S△ACB=$\frac{1}{2}$×2$\sqrt{5}$×2$\sqrt{5}$=10,
∴$\frac{{S}_{△ABC}}{{S}_{△EFD}}$=($\frac{AC}{ED}$)2.
点评 本题考查了作图-轴对称变换:几何图形都可看做是有点组成,我们在画一个图形的轴对称图形时,可以确定一些特殊的对称点.也考查了对称轴的性质.

| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 对角线相等且互相垂直的四边形是正方形 | |
| C. | 平分弦的直径垂直于弦,并且平分弦所对的弧 | |
| D. | 三角形任意两边之差小于第三边 |
 已知:如图所示,AB∥CD,∠A=∠F,∠D=∠E.求证:AF⊥DE.
已知:如图所示,AB∥CD,∠A=∠F,∠D=∠E.求证:AF⊥DE.
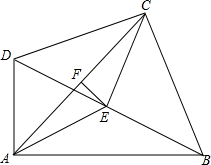 如图,在四边形ABCD中,∠DCB=∠DAB=Rt∠,点E是对角线BD的中点.
如图,在四边形ABCD中,∠DCB=∠DAB=Rt∠,点E是对角线BD的中点.