题目内容
5．
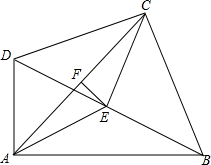如图，在四边形ABCD中，∠DCB=∠DAB=Rt∠，点E是对角线BD的中点．（1）试说明AE=CE的理由；
（2）若点F是AC的中点，试判断EF与AC的位置关系．
分析 （1）根据直角三角形斜边上的中线等于斜边的一半得到AE=$\frac{1}{2}$BD，CE=$\frac{1}{2}$BD，证明结论；
（2）根据等腰三角形的三线合一证明即可．
解答 解：（1）∵∠DCB=∠DAB=Rt∠，点E是对角线BD的中点，
∴AE=$\frac{1}{2}$BD，CE=$\frac{1}{2}$BD，
∴AE=CE；
（2）∵AE=CE，点F是AC的中点，
∴EF⊥AC．
点评 本题考查的是直角三角形的性质和等腰三角形的性质，掌握直角三角形斜边上的中线等于斜边的一半、等腰三角形的三线合一是解题的关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
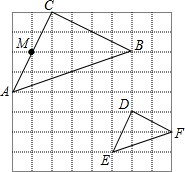如图，在8×8的正方形网格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上，AC与网格上的直线相交于点M．
把两根钢条AA、BB的中点连在一起，可以做成一个测量工件内槽宽工具（卡钳），如图，若得AB=6厘米，则槽宽为6厘米．